题目内容
在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(Ⅰ)求证:{an-n}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设数列{an}的前n项和Sn,求Sn+1-Sn的最大值.
(Ⅰ)求证:{an-n}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设数列{an}的前n项和Sn,求Sn+1-Sn的最大值.
考点:数列的求和,等比数列的性质,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)整理题设an+1=4an-3n+1得an+1-(n+1)=4(an-n),进而可推断数列{an-n}是等比数列;
(Ⅱ)由(Ⅰ)可数列{an-n}的通项公式,再求出数列{an}的通项公式an;
(Ⅲ)由(Ⅱ)中求得an,根据等比和等差数列的求和公式求得Sn,代入Sn+1-4Sn整理后根据-
(3n2+n-4)和二次函数的性质,求出最大值.
(Ⅱ)由(Ⅰ)可数列{an-n}的通项公式,再求出数列{an}的通项公式an;
(Ⅲ)由(Ⅱ)中求得an,根据等比和等差数列的求和公式求得Sn,代入Sn+1-4Sn整理后根据-
| 1 |
| 2 |
解答:
(Ⅰ)证明:由题设得an+1=4an-3n+1,则an+1-(n+1)=4(an-n),n∈N*.
又a1-1=1,所以数列{an-n}是首项为1,且公比为4的等比数列.
(Ⅱ)解:由(Ⅰ)可知an-n=4n-1,于是数列{an}的通项公式为an=4n-1+n.
(Ⅲ)解:由(Ⅱ)得,an=4n-1+n,
所以数列{an}的前n项和Sn=
+
=
+
,
则Sn+1-Sn=
+
-[
+
]
=-
(3n2+n-4),
由n∈N*得,当n=1时,-
(3n2+n-4)的最大值是0,
所以Sn+1-Sn的最大值是0.
又a1-1=1,所以数列{an-n}是首项为1,且公比为4的等比数列.
(Ⅱ)解:由(Ⅰ)可知an-n=4n-1,于是数列{an}的通项公式为an=4n-1+n.
(Ⅲ)解:由(Ⅱ)得,an=4n-1+n,
所以数列{an}的前n项和Sn=
| 1-4n |
| 1-4 |
| n(1+n) |
| 2 |
| 4n-1 |
| 3 |
| n(1+n) |
| 2 |
则Sn+1-Sn=
| 4n+1-1 |
| 3 |
| (n+1)(2+n) |
| 2 |
| 4n-1 |
| 3 |
| n(1+n) |
| 2 |
=-
| 1 |
| 2 |
由n∈N*得,当n=1时,-
| 1 |
| 2 |
所以Sn+1-Sn的最大值是0.
点评:本题以数列的递推关系式为载体,主要考查等比数列的概念、等比数列的通项公式及前n项和公式、不等式的证明等基础知识,考查运算能力和推理论证能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
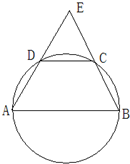 如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.