题目内容
对于两个定义域相同的函数f(x)、g(x),若存在实数m,n使得h(x)=mf(x)+ng(x),则称函数h(x)是“函数f(x),g(x)的一个线性表达”.
(1)若h(x)=2x2+3x-1是“函数f(x)=x2+ax,g(x)=x+b(a,b∈R,ab≠0)的一个线性表达”,求a+2b的取值范围;
(2)若函数h(x)是“函数f(x)=log4(4x+1),g(x)=x-1的一个线性表达”且满足:①h(x)是偶函数;②g(x)的最小值是1,求h(x)的解析式.
(1)若h(x)=2x2+3x-1是“函数f(x)=x2+ax,g(x)=x+b(a,b∈R,ab≠0)的一个线性表达”,求a+2b的取值范围;
(2)若函数h(x)是“函数f(x)=log4(4x+1),g(x)=x-1的一个线性表达”且满足:①h(x)是偶函数;②g(x)的最小值是1,求h(x)的解析式.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)依题意列出等式2x2+3x-1=m(x2+ax)+n(x+b),化简整理后由系数相等得到a,b的关系,代入a+2b后由绝对值的不等式求得答案;
(2)依题意知:h(x)=mlog4(4x+1)+n(x-1)是偶函数,由偶函数的性质列式得到m与n的关系,再由
g(x)的最小值是1求得n的值,则h(x)的解析式可求.
(2)依题意知:h(x)=mlog4(4x+1)+n(x-1)是偶函数,由偶函数的性质列式得到m与n的关系,再由
g(x)的最小值是1求得n的值,则h(x)的解析式可求.
解答:
解:依题意知:2x2+3x-1=m(x2+ax)+n(x+b)=mx2+(am+n)x+nb,
∴
,即2a-
=3.
得:a=
+
,a≠0.
∴b≠-
.
∴a+2b=2b+
+
.
∵|2b+
|=|2b|+|
|≥2.
∴2b+
≥2或2b+
≤-2且2b+
≠-
.
∴a+2b的取值范围是(-∞,-
)∪(-
,-
]∪[
,+∞);
(2)依题意知:h(x)=mlog4(4x+1)+n(x-1)是偶函数,
故h(-x)=h(x),
即mlog4(4-x+1)+n(-x-1)=mlog4(4x+1)+n(x-1),
整理得:m=-2n,
∴h(x)=mlog4(4x+1)+n(x-1)=-2nlog4(4x+1)+n(x-1)
=-nlog2(2x+2-x)-n.
∵2x+2-x≥2,
∴log2(2x+2-x)≥1.
由于h(x)的最小值是1,
∴n<0,-nlog2(2x+2-x)-n≥-2n=1.
故n=-
.
∴h(x)=
log2(2x+2-x)+
.
∴
|
| 1 |
| b |
得:a=
| 3 |
| 2 |
| 1 |
| 2b |
∴b≠-
| 1 |
| 3 |
∴a+2b=2b+
| 1 |
| 2b |
| 3 |
| 2 |
∵|2b+
| 1 |
| 2b |
| 1 |
| 2b |
∴2b+
| 1 |
| 2b |
| 1 |
| 2b |
| 1 |
| 2b |
| 13 |
| 6 |
∴a+2b的取值范围是(-∞,-
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 7 |
| 2 |
(2)依题意知:h(x)=mlog4(4x+1)+n(x-1)是偶函数,
故h(-x)=h(x),
即mlog4(4-x+1)+n(-x-1)=mlog4(4x+1)+n(x-1),
整理得:m=-2n,
∴h(x)=mlog4(4x+1)+n(x-1)=-2nlog4(4x+1)+n(x-1)
=-nlog2(2x+2-x)-n.
∵2x+2-x≥2,
∴log2(2x+2-x)≥1.
由于h(x)的最小值是1,
∴n<0,-nlog2(2x+2-x)-n≥-2n=1.
故n=-
| 1 |
| 2 |
∴h(x)=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了函数奇偶性的性质,考查了数学转化思想方法,关键是对题意的理解,是中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
某地固定电话市话收费规定:前三分钟0.20元(不满三分钟按三分钟计算),以后每加一分钟增收0.10元 (不满一分钟按一分钟计算),那么某人打市话550秒,应支付电话费( )
| A、1.00元 |
| B、0.90元 |
| C、1.20元 |
| D、0.80元 |
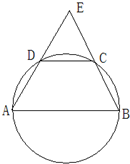 如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.