题目内容
已知函数f(x)=|x-2|-|x-5|.
(Ⅰ)证明:|f(x)|≤3;
(Ⅱ)若函数g(x)=f(x)-logax(a>0且a≠1)有两个零点,求a的值.
(Ⅰ)证明:|f(x)|≤3;
(Ⅱ)若函数g(x)=f(x)-logax(a>0且a≠1)有两个零点,求a的值.
考点:绝对值不等式的解法,函数零点的判定定理
专题:函数的性质及应用
分析:(Ⅰ)f(x)=|x-2|-|x-5|=
,易求其值域为[-3,3],从而可证|f(x)|≤3;
(Ⅱ)由函数零点的判定定理可知,y=logax,(a>0且a≠1)与函数y=f(x)的图象有两个交点,且函数y=logax,(a>0且a≠1)的图象经过点(5,3),从而可求得a的值.
|
(Ⅱ)由函数零点的判定定理可知,y=logax,(a>0且a≠1)与函数y=f(x)的图象有两个交点,且函数y=logax,(a>0且a≠1)的图象经过点(5,3),从而可求得a的值.
解答:
(I)证明:f(x)=|x-2|-|x-5|=
,其值域为[-3,3],即|f(x)|≤3;
(II)解:依题意y=logax,(a>0且a≠1)与函数y=f(x)的图象有两个交点,

则函数y=logax,(a>0且a≠1)的图象经过点(5,3),
所以3=loga5得a=
.
|
(II)解:依题意y=logax,(a>0且a≠1)与函数y=f(x)的图象有两个交点,

则函数y=logax,(a>0且a≠1)的图象经过点(5,3),
所以3=loga5得a=
| 3 | 5 |
点评:本题考查绝对值不等式的解法,考查函数零点的判定定理,考查作图与运算求解能力,属于中档题.

练习册系列答案
相关题目
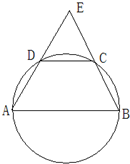 如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.