题目内容
14.不论m为何实数,直线mx-y+3+m=0恒过定点(-1,3).分析 直线mx-y+3+m=0化为:m(x+1)+(3-y)=0,令$\left\{\begin{array}{l}{x+1=0}\\{3-y=0}\end{array}\right.$,解出即可得出.
解答 解:直线mx-y+3+m=0化为:m(x+1)+(3-y)=0,
令$\left\{\begin{array}{l}{x+1=0}\\{3-y=0}\end{array}\right.$,解得x=-1,y=3.
∴直线恒过定点(-1,3).
故答案为:(-1,3).
点评 本题考查了直线系的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.下列求导数运算正确的是( )
| A. | ${(x+\frac{1}{x})^'}=1+\frac{1}{x^2}$ | B. | (lgx)′=$\frac{1}{xlge}$ | C. | (3x)′=3xln3 | D. | (x2cosx)′=-2xsinx |
2.已知等比数列{an}的前n项和为Sn,且S2+a2,S1+2a2,S3+a3,成等差数列,则数列{an}的公比为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
9.若集合A={-2,-1,0,1,2},B={x||x|≤1},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1} | C. | {x|-1≤x≤1} | D. | {x|0≤x≤1} |
6.函数g(x)=-x2+2lnx的图象大致是( )
| A. |  | B. | 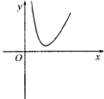 | C. | 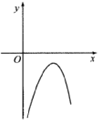 | D. | 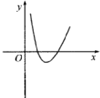 |