题目内容
已知顶点为原点O的抛物线 的焦点
的焦点 与椭圆
与椭圆 的右焦点重合
的右焦点重合
 与
与 在第一和第四象限的交点分别为A、B.
在第一和第四象限的交点分别为A、B.
(1) 若△AOB是边长为 的正三角形,求抛物线
的正三角形,求抛物线 的方程;
的方程;
(2)若 ,求椭圆
,求椭圆 的离心率
的离心率 ;
;
(3) 点 为椭圆
为椭圆 上的任一点,若直线
上的任一点,若直线 、
、 分别与
分别与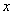 轴交于点
轴交于点 和
和 ,证明:
,证明: .
.
解:(1)设椭圆的右焦点为 ,依题意得抛物线的方程为
,依题意得抛物线的方程为
∵△ 是边长为
是边长为 的正三角形,
的正三角形,
∴点A的坐标是 ,
,
代入抛物线的方程 解得
解得 ,
,
故所求抛物线 的方程为
的方程为
(2)∵ , ∴ 点
, ∴ 点 的横坐标是
的横坐标是
代入椭圆方程解得 ,即点
,即点 的坐标是
的坐标是
∵ 点 在抛物线
在抛物线 上,
上,
∴ ,
,
将 代入上式整理得:
代入上式整理得: ,
,
即 ,解得
,解得
∵  ,故所求椭圆
,故所求椭圆 的离心率
的离心率 。
。
(3)证明:设 ,代入椭圆方程得
,代入椭圆方程得

而直线 的方程为
的方程为
令 得
得 。
。
在 中,以
中,以 代换
代换 得
得
∴ 


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和
和 ,定义
,定义 ,若平面向量
,若平面向量 满足:
满足: ,
, 与
与 的夹角
的夹角 ,且
,且 和
和 都在集合
都在集合 中,
中, .
. 是
是 椭圆的一个焦点,
椭圆的一个焦点, 是短轴的一个端点,线段
是短轴的一个端点,线段 的延长线交
的延长线交 ,且
,且 ,则
,则 的离心率为 .
的离心率为 . B.
B.  C.
C.  D.
D. 

 尺 B.
尺 B. 尺 C.
尺 C. 尺 D.
尺 D. 尺
尺
 的边长为
的边长为 ,
, ,
,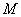 为
为 的中点,若
的中点,若 为菱形内任意一点(含边界),则
为菱形内任意一点(含边界),则 的最大值为( )
的最大值为( )
 B.
B.  C. 9 D.6
C. 9 D.6 (
(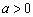 ),若
),若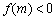 ,则
,则 与0的大小关系 。
与0的大小关系 。