题目内容
11.已知函数f(x)=ax3-3x2+1,若f(-a)、f(a)、f(3a)成公差不为0的等差数列,则过坐标原点作曲线y=f(x)的切线可以作( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
分析 先求出a,再分类讨论,求出切线的条数.
解答 解:∵f(-a)、f(a)、f(3a)成公差不为0的等差数列,
∴2f(a)=f(-a)+f(3a),
代入化简可得a4-a2=0,
∵a≠0,∴a=±1,
a=-1,函数f(x)=-x3-3x2+1,
设切点A(x0,y0),
∵f′(x)=-3x2-6x,
∴切线斜率为-3x02-6x0,又切线过原点,
∴-y0=3x03+6x02①
又∵切点A(x0,y0)在f(x)=-x3-3x2+1的图象上,
∴y0=-x03-3x02+1②
由①②得:2x03+3x02+1=0,方程有唯一解;
a=1,函数f(x)=x3-3x2+1,
设切点A(x0,y0),
∵f′(x)=3x2-6x,
∴切线斜率为3x02-6x0,又切线过原点,
∴-y0=-3x03+6x02①
又∵切点A(x0,y0)在f(x)=x3-3x2+1的图象上,
∴y0=x03-3x02+1②
由①②得:2x03-3x02-1=0,方程有唯一解;
故选C.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查等差数列的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.如图所示的程序框图,运行程序后,输出的结果为( )


| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
6.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>1}\\{(\frac{1}{2})^{x},x≤1}\end{array}\right.$,则f(f(-2))=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
3.已知一几何体的三视图如图所示,则该几何体的表面积为( )
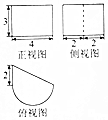

| A. | 14+6$\sqrt{5}$+10π | B. | 14+6$\sqrt{5}$+20π | C. | 12+12π | D. | 26+6$\sqrt{5}$+10π |
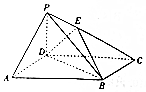 如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.