题目内容
19.已知数列{an}满足:点(n,an)在直线2x-y+1=0上,若使a1、a4、am构成等比数列,则m=13.分析 由题意可得an=2n+1,再根据a1、a4、am构成等比数列,即可求出m的值.
解答 解:点(n,an)在直线2x-y+1=0上,
∴an=2n+1,
∴a1=3,a4=9,am=2m+1,
∵a1、a4、am构成等比数列,
∴92=3(2m+1),
解得m=13,
故答案为:13.
点评 本题考查了等差数列和等比数列的性质,属于基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{4}x+1,x≤1}\\{lnx,x>1}\end{array}\right.$,则方程f(x)=ax恰有两个不同的实数根时,实数a的取值范围是( )
| A. | (0,$\frac{1}{e}$) | B. | [$\frac{1}{4}$,$\frac{1}{e}$) | C. | (0,$\frac{1}{4}$] | D. | ($\frac{1}{4}$,e) |
7.下列各区间中,是函数f(x)=2cos2x的一个单调递增区间的为( )
| A. | (0,$\frac{π}{2}$) | B. | ($\frac{π}{2}$,π) | C. | (-$\frac{π}{4}$,$\frac{π}{4}$) | D. | ($\frac{π}{4}$,$\frac{3π}{4}$) |
14.设集合A={x|x(x+1)≤0},集合B={x|2x>1},则集合A∪B等于( )
| A. | {x|x≥0} | B. | {x|x≥-1} | C. | {x|x>0} | D. | {x|x>-1} |
9.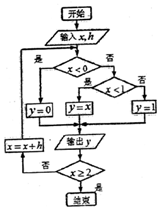 如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )
如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )
 如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )
如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )| A. | 1 | B. | 1.5 | C. | 2.5 | D. | 3 |
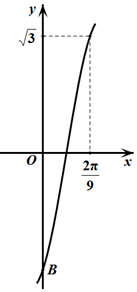 已知函数f(x)=4sin$\frac{ω}{2}xcos({\frac{ω}{2}x-\frac{π}{3}})-\sqrt{3}$(ω>0).
已知函数f(x)=4sin$\frac{ω}{2}xcos({\frac{ω}{2}x-\frac{π}{3}})-\sqrt{3}$(ω>0).