题目内容
2.已知x,y,z,a,b,c,k均为正数,且x2+y2+z2=10,a2+b2+c2=90,ax+by+cz=30,a+b+c=k(x+y+z),则k=( )| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 9 |
分析 根据所给条件,利用柯西不等式求解,利用等号成立的条件即可.
解答 解:因为x2+y2+z2=10,a2+b2+c2=90,ax+by+cz=30,
所以(a2+b2+c2)(x2+y2+z2)=(ax+by+cz)2,
又(a2+b2+c2)(x2+y2+z2)≥(ax+by+cz)2等号成立,
当且仅当$\frac{a}{x}$=$\frac{b}{y}$=$\frac{c}{z}$=k,
则a=kx,b=ky,c=kz,代入a2+b2+c2=90,
得k2(x2+y2+z2)=90,
于是k=3,
故选:C.
点评 柯西不等式的特点:一边是平方和的积,而另一边为积的和的平方,因此,当欲证不等式的一边视为“积和结构”或“平方和结构”,再结合不等式另一边的结构特点去尝试构造.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
7.设曲线y=2016xn+1(n∈N*)在点(1,2016)处的切线与x轴交点的横坐标为xn,令an=log2016xn,则a1+a2+…+a2015的值为( )
| A. | 2016 | B. | 2015 | C. | 1 | D. | -1 |
14.将45化为二进制正确的是( )
| A. | 111001 | B. | 110111 | C. | 101101 | D. | 111011 |
11.下面四个条件中,使a>b成立的充要条件是( )
| A. | |a|>|b| | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a2>b2 | D. | 2a>2b |
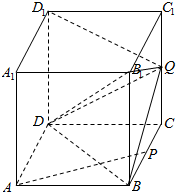 如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.