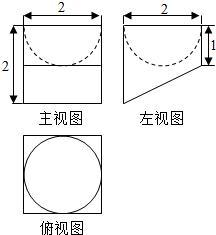
题目内容
20.过原点作一条倾斜角为θ的直线与椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$交于A、B两点,F为椭圆的左焦点,若AF⊥BF,且该椭圆的离心率$e∈[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{6}}}{3}}]$,则θ的取值范围为$[{\frac{π}{6},\frac{5π}{6}}]$.分析 设右焦点F′,连结AF′,BF′,得四边形AFBF′是正方形,推导出$\frac{c}{a}$=$\frac{1}{sin\frac{θ}{2}+cos\frac{θ}{2}}$=$\frac{1}{\sqrt{2}sin(\frac{θ}{2}+\frac{π}{4})}$,由此根据该椭圆的离心率$e∈[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{6}}}{3}}]$,能求出θ的取值范围.
解答 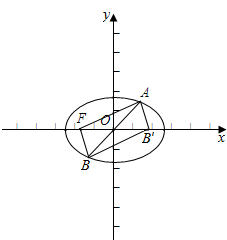 解:设右焦点F′,连结AF′,BF′,得四边形AFBF′是正方形,
解:设右焦点F′,连结AF′,BF′,得四边形AFBF′是正方形,
∵AF+AF′=2a,AF+BF=2a,OF=c,∴AB=2c,
∵∠BAF=$\frac{1}{2}$θ,∴AF=2c•cos$\frac{θ}{2}$,BF=2c•sin$\frac{θ}{2}$,
∴2csin$\frac{θ}{2}$+2ccos$\frac{θ}{2}$=2a,
∴$\frac{c}{a}$=$\frac{1}{sin\frac{θ}{2}+cos\frac{θ}{2}}$=$\frac{1}{\sqrt{2}sin(\frac{θ}{2}+\frac{π}{4})}$,
∵该椭圆的离心率$e∈[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{6}}}{3}}]$,
∴$\frac{\sqrt{2}}{2}≤\frac{1}{\sqrt{2}sin(\frac{θ}{2}+\frac{π}{4})}≤\frac{\sqrt{6}}{3}$,
∵θ∈[0,π),∴$\frac{π}{6}≤θ≤\frac{5π}{6}$.
∴θ的取值范围是[$\frac{π}{6}$,$\frac{5π}{6}$].
故答案为:[$\frac{π}{6}$,$\frac{5π}{6}$].
点评 求椭圆离心率的范围首先要根据椭圆的几何性质找到关于a,b,c的关系式,求解即可得到离心率范围.

| A. | 98 | B. | 105 | C. | 112 | D. | 119 |
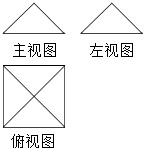 一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )
一个几何体的三视图如图所示,主视图与左视图都是腰长为5底为8的等腰三角形,俯视图是边长为8的正方形,那么此几何体的侧面积为( )| A. | 48 | B. | 64 | C. | 80 | D. | 120 |
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | b<c<a |
| A. | $\frac{3+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{3-i}{2}$ | D. | $\frac{-3-i}{2}$ |