题目内容
10.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,直线y=$\frac{1}{2}$被椭圆E截得的线段长为$\sqrt{6}$.(Ⅰ)求椭圆E的方程;
(Ⅱ)若椭圆E两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称,求实数m的取值范围.
分析 (Ⅰ)由题设得,椭圆过点$({\frac{{\sqrt{6}}}{2},\frac{1}{2}})$,代入椭圆方程,结合离心率公式和a,b,c的关系,解方程可得椭圆方程;
(Ⅱ)由(Ⅰ)易得知m≠0,可设直线AB的方程为$y=-\frac{1}{m}x+b$.代入椭圆方程,运用韦达定理和判别式大于0,结合中点坐标公式,解不等式即可得到所求范围.
解答 解:(Ⅰ)由题设得,椭圆过点$({\frac{{\sqrt{6}}}{2},\frac{1}{2}})$,
所以$\left\{{\begin{array}{l}{\frac{3}{{2{a^2}}}+\frac{1}{{4{b^2}}}=1}\\{\frac{c}{a}=\frac{{\sqrt{2}}}{2}}\\{{a^2}={b^2}+{c^2}}\end{array}}\right.$,
解得a=$\sqrt{2}$,b=1,c=1,
所以椭圆的方程为$\frac{x^2}{2}+{y^2}=1$;
(Ⅱ)由(Ⅰ)易得知m≠0,可设直线AB的方程为$y=-\frac{1}{m}x+b$.
由$\left\{{\begin{array}{l}{y=-\frac{1}{m}x+b}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$消去y得$(\frac{1}{2}+\frac{1}{m^2}){x^2}-\frac{2b}{m}x+{b^2}-1=0$•
因为直线y=mx+$\frac{1}{2}$与椭圆$\frac{x^2}{2}+{y^2}=1$有两个不同交点,
所以$△=-2{b^2}+2+\frac{4}{m^2}>0$•①
设A(x1,y1),B(x2,y2),由韦达定理知,${x_1}+{x_2}=\frac{4mb}{{{m^2}+2}}$,
于是线段AB的中点坐标为$M(\frac{2mb}{{{m^2}+2}},\frac{{{m^2}b}}{{{m^2}+2}})$,
将其代入直线$y=mx+\frac{1}{2}$,解得$b=-\frac{{{m^2}+2}}{{2{m^2}}}$②
将②代入①,得$\frac{1}{m^4}-\frac{1}{m^2}-\frac{3}{4}<0$,
解得$m<-\frac{{\sqrt{6}}}{3}$或$m>\frac{{\sqrt{6}}}{3}$.
因此,所求实数m的取值范围$(-∞,-\frac{{\sqrt{6}}}{3})∪(\frac{{\sqrt{6}}}{3},+∞)$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质和离心率公式,考查直线和椭圆的位置关系,注意运用对称性,设出直线方程,联立椭圆方程,运用韦达定理和判别式大于0,考查运算能力,属于中档题.

| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{2\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{7}$ | D. | $\frac{{2\sqrt{21}}}{7}$ |
| A. | 6 | B. | 5 | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
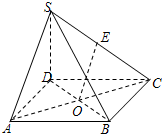 如图四棱锥S-ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6.
如图四棱锥S-ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6. 已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.
已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.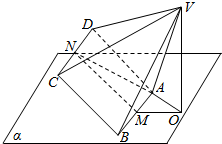 如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )
如图,底面为正方形且各侧棱长均相等的四棱锥V-ABCD可绕着棱AB任意旋转,若AB?平面α,M、N分别是AB、CD的中点,AB=2,VA=$\sqrt{5}$,点V在平面α上的射影为点O,则当ON的最大时,二面角C-AB-O的大小是( )