题目内容
已知函数f(x)=
x3+x2-2ax-1,f′(-1)=0.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)如果对于任意的x∈[-2,0),都有f(x)≤bx+3,求b的取值范围.
| a |
| 3 |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)如果对于任意的x∈[-2,0),都有f(x)≤bx+3,求b的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由f′(x)=ax2+2x-2a,且f′(-1)=0,得a=-2,从而f′(x)=-2x2+2x+4=-2(x+1)(x-2),得(x)在(-∞,-1)和(2,+∞)上单调递减,在(-1,2)上单调递增,
(Ⅱ) 因为对于任意的x∈[-2,0),都有f(x)≤bx+3,即bx+3≥-
x3+x2+4x-1,得b≤-
x2+x+4-
,设h(x)=-
x2+x+4-
,从而h′(x)=-
x+1+
,
又x∈[-2,)),得h′(x)>0,从而h(x)在[-2,0)上单调递增,进而b≤
.
(Ⅱ) 因为对于任意的x∈[-2,0),都有f(x)≤bx+3,即bx+3≥-
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| x |
| 2 |
| 3 |
| 4 |
| x |
| 4 |
| 3 |
| 4 |
| x2 |
又x∈[-2,)),得h′(x)>0,从而h(x)在[-2,0)上单调递增,进而b≤
| 4 |
| 3 |
解答:
解:(Ⅰ)∵f′(x)=ax2+2x-2a,且f′(-1)=0,
∴a=-2,
∴f′(x)=-2x2+2x+4=-2(x+1)(x-2).
令f′(x)=0,解得x1=-1,x2=2,
随着x的变化,f′(x)和f(x)的变化情况如下:
即f(x)在(-∞,-1)和(2,+∞)上单调递减,在(-1,2)上单调递增,
(Ⅱ) 因为对于任意的x∈[-2,0),都有f(x)≤bx+3,
即bx+3≥-
x3+x2+4x-1,
∴b≤-
x2+x+4-
,
设h(x)=-
x2+x+4-
,
∴h′(x)=-
x+1+
,
又∵x∈[-2,)),
∴-
x>0,
>0,
∴h′(x)>0,
∴h(x)在[-2,0)上单调递增,
∴h(x)min=h(-2)=
,
∴b≤
.
∴a=-2,
∴f′(x)=-2x2+2x+4=-2(x+1)(x-2).
令f′(x)=0,解得x1=-1,x2=2,
随着x的变化,f′(x)和f(x)的变化情况如下:
| x | (-∞,-1) | -1 | (-1,2) | 2 | (2,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | ↗ | ↘ |
(Ⅱ) 因为对于任意的x∈[-2,0),都有f(x)≤bx+3,
即bx+3≥-
| 2 |
| 3 |
∴b≤-
| 2 |
| 3 |
| 4 |
| x |
设h(x)=-
| 2 |
| 3 |
| 4 |
| x |
∴h′(x)=-
| 4 |
| 3 |
| 4 |
| x2 |
又∵x∈[-2,)),
∴-
| 4 |
| 3 |
| 4 |
| x2 |
∴h′(x)>0,
∴h(x)在[-2,0)上单调递增,
∴h(x)min=h(-2)=
| 4 |
| 3 |
∴b≤
| 4 |
| 3 |
点评:本题考查了函数的单调性,函数的最值问题,参数的取值,考查导数的应用,是一道综合题.

练习册系列答案
相关题目
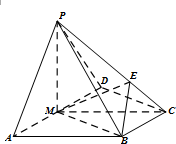 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD是直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD是直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=
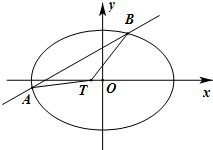 如图,椭圆C:
如图,椭圆C: