题目内容
(1)求函数f(x)=(x-
)0+
的定义域;
(2)已知函数f(x)是二次函数,且f(x+1)+f(x)=2x2-4x+4,求f(x)的表达式;
(3)求函数f(x)=x-
的值域.
| 1 |
| 2 |
| 1 | ||
|
(2)已知函数f(x)是二次函数,且f(x+1)+f(x)=2x2-4x+4,求f(x)的表达式;
(3)求函数f(x)=x-
| 1-2x |
考点:函数的定义域及其求法,函数的值域,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)由题意得不等式组,解出即可;
(2).由已知设f(x)=ax2+bx+c(a≠0),f(x+1)+f(x)=2ax2+(2a+2b)x+a+b+2c=2x2-4x+4,比较对应系数得方程组解出即可;
(3)通过换元法求出函数的值域问题.
(2).由已知设f(x)=ax2+bx+c(a≠0),f(x+1)+f(x)=2ax2+(2a+2b)x+a+b+2c=2x2-4x+4,比较对应系数得方程组解出即可;
(3)通过换元法求出函数的值域问题.
解答:
解:(1).要是函数有意义,则:
,解得:x>-2且x≠
,
所以,函数的定义域为:(-2,
)∪(
,+∞)
(2).由已知设f(x)=ax2+bx+c(a≠0),
则:f(x+1)=a(x+1)2+b(x+1)+c=ax2+(2a+b)x+a+b+c
所以f(x+1)+f(x)=2ax2+(2a+2b)x+a+b+2c=2x2-4x+4
比较对应系数有:
,解得:a=1,b=-3,c=3
所以f(x)=x2-3x+3;
(3)令
=t≥0∴x=
,
所以y=f(t)=-
-t+
=-
(t+1)2+1(t≥0)∴y∈(-∞,
].
|
| 1 |
| 2 |
所以,函数的定义域为:(-2,
| 1 |
| 2 |
| 1 |
| 2 |
(2).由已知设f(x)=ax2+bx+c(a≠0),
则:f(x+1)=a(x+1)2+b(x+1)+c=ax2+(2a+b)x+a+b+c
所以f(x+1)+f(x)=2ax2+(2a+2b)x+a+b+2c=2x2-4x+4
比较对应系数有:
|
所以f(x)=x2-3x+3;
(3)令
| 1-2x |
| 1-t2 |
| 2 |
所以y=f(t)=-
| t2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了函数的定义域,函数的值域问题,求函数的解析式问题,是一道基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知全集U={2011,2012,2013,2014,2015},M={2011,2012,2013},则∁UM=( )
| A、{2014} |
| B、{2014,2015} |
| C、{2011,2012,2013} |
| D、{2011,2012,2013,2014,2015} |
如果角θ的终边经过点P(-
,
),那么tanθ等于( )
| ||
| 2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
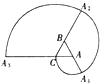 如图,一条螺旋线是用以下方法画成的:△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3是分别以A、B、C为圆心,AC、BA1、CA2为半径画的圆弧,曲线CA1A2A3称为螺旋线的第一圈,然后又以A为圆心,AA3为半径画圆弧…这样画到第n圈,则所得螺旋线的长度ln为( )
如图,一条螺旋线是用以下方法画成的:△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3是分别以A、B、C为圆心,AC、BA1、CA2为半径画的圆弧,曲线CA1A2A3称为螺旋线的第一圈,然后又以A为圆心,AA3为半径画圆弧…这样画到第n圈,则所得螺旋线的长度ln为( )| A、(3n2+n)π | ||
| B、(3n2-n+1)π | ||
C、
| ||
D、
|
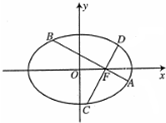 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆