题目内容
4．已知cosα=$\frac{1}{2}$，且α是第四象限的角，求sinα和tanα．分析 由条件利用同角三角函数的基本关系，求得sinα和tanα的值．
解答 解：∵cosα=$\frac{1}{2}$，且α是第4象限角，
∴sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{\sqrt{3}}{2}$，
∴tanα=$\frac{sinα}{cosα}$=-$\sqrt{3}$．
点评 本题主要考查同角三角函数的基本关系、三角函数在各个象限中的符号，属于基础题．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
15．若不等式x+$\sqrt{xy}$≤a（x+2y）对任意的正实数x，y都成立，则实数a的最小值是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{\sqrt{6}+2}{4}$ | C． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | D． | $\frac{\sqrt{2}+2}{4}$ |
19．函数f（x）的图象如图所示，则下列结论正确的是（ ）
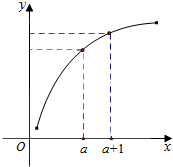
| A． | 0＜f′（a）＜f′（a+1）＜f（a+1）-f（a） | B． | 0＜f′（a+1）＜f（a+1）-f（a）＜f′（a） | ||
| C． | 0＜f′（a+1）＜f′（a）＜f（a+1）-f（a） | D． | 0＜f（a+1）-f（a）＜f′（a）＜f′（a+1） |