题目内容
双曲线C:
-y2=1的两条渐近线夹角(锐角)为θ,则tanθ=( )
| x2 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,求得斜率,再由两直线的夹角公式,计算即可得到.
解答:
解:双曲线C:
-y2=1的两条渐近线分别为
y=±
x,
则斜率分别为-
,
.
由两直线的夹角公式可得,
tanθ=|
|=
.
故选:D.
| x2 |
| 4 |
y=±
| 1 |
| 2 |
则斜率分别为-
| 1 |
| 2 |
| 1 |
| 2 |
由两直线的夹角公式可得,
tanθ=|
| ||||
1+
|
| 4 |
| 3 |
故选:D.
点评:本题考查双曲线的方程和性质,主要考查渐近线方程的运用,运用两直线的夹角公式计算是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
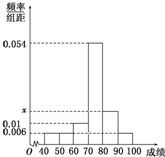 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是: