题目内容
正方形ABCD中，E是BC边延长线上的一点，AE交CD于点F，FN∥AD交DE于N，求证：CF=NF．
考点：平行线分线段成比例定理
专题：选作题,立体几何
分析：利用△ENF∽△EDA，可得
=
，△EFC∽△EAB，可得
=
，即可证明结论．
| NF |
| DA |
| EF |
| EA |
| CF |
| AB |
| EF |
| EA |
解答：
证明：∵ABCD是正方形，∴DA=AB、FC∥AB．
∵NF∥DA，∴△ENF∽△EDA，∴
=
．
∵FC∥AB，∴△EFC∽△EAB，∴
=
，
∴
=
，又AB=DA，∴CF=NF．
∵NF∥DA，∴△ENF∽△EDA，∴
| NF |
| DA |
| EF |
| EA |
∵FC∥AB，∴△EFC∽△EAB，∴
| CF |
| AB |
| EF |
| EA |
∴
| CF |
| AB |
| NF |
| DA |
点评：本题考查平行线分线段成比例定理，考查三角形相似的证明与运用，比较基础．
练习册系列答案
相关题目
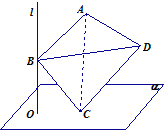如图，直线l⊥平面α，垂足为O，正四面体ABCD的棱长为2，点C在平面内，B是直线l上的动点，则当O到AD的距离为最大时，正四面体在平面α上的射影面积为（ ）
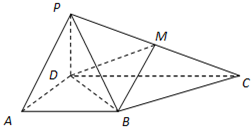如图，四棱锥P-ABCD中，底面ABCD为梯形，∠DAB=60°，AB∥CD，AD=CD=2AB，PD⊥底面ABCD，M为PC的中点．