Question

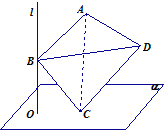如图，直线l⊥平面α，垂足为O，正四面体ABCD的棱长为2，点C在平面内，B是直线l上的动点，则当O到AD的距离为最大时，正四面体在平面α上的射影面积为（　　）

• A、

  2+ 2

  2

• B、

  2 +1

  2

• C、1
• D、

  3

Answer 1

考点：平行投影及平行投影作图法

专题：空间位置关系与距离

分析：确定直线BC与动点O的空间关系，得到最大距离为AD到球心的距离+半径，再考虑取得最大距离时四面体的投影情况，即可求得结论．

解答： 解：由题意，直线BC与动点O的空间关系：点O是以BC为直径的球面上的点，所以O到AD的距离为四面体上以BC为直径的球面上的点到AD的距离，最大距离为AD到球心的距离（即BC与AD的公垂线）+半径=

2

+1．
再考虑取得最大距离时四面体的投影情况，此时我们注意到AD垂直平面OBC，且平行平面α，故其投影是以AD为底，O到AD的距离投影，即（

2

+1）cos45°=

1

2

+

2

2

为高的等腰三角形，其面积=

1

2

×2×（

1

2

+

2

2

）=

1

2

+

2

2

．
故选A．

点评：本题考查点、线、面间的距离计算，考查学生分析解决问题的能力，属于中档题．