题目内容
已知关于x的方程x2-2ax+a+2=0的两根满足1＜x1＜4且1＜x2＜4，求实数a的取值范围．
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：利用方程和函数之间的关系，转化为一元二次函数根的分布问题，即可得到结论．
解答：
解：设f（x）=x2-2ax+a+2，
∵方程x2-2ax+a+2=0的两根满足1＜x1＜4且1＜x2＜4，
∴
，
即
，∴
，
即2≤a＜
，
∴实数a的取值范围是2≤a＜
．
∵方程x2-2ax+a+2=0的两根满足1＜x1＜4且1＜x2＜4，
∴
|
即
|
|
即2≤a＜
| 18 |
| 7 |
∴实数a的取值范围是2≤a＜
| 18 |
| 7 |
点评：本题主要考查一元二次方程根的分布问题，将方程转化为函数是解决本题的关键．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
设1＜x＜2，则
、(
)2、
的大小关系是（ ）
| lnx |
| x |
| lnx |
| x |
| lnx2 |
| x2 |
A、(
| ||||||
B、
| ||||||
C、(
| ||||||
D、
|
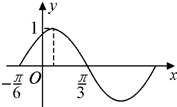函数f（x）=sin（ωx+φ），（x∈R）（ω＞0，|φ|＜