题目内容
已知f(x)=cosx(cosx-3)+sinx(sinx-3),若x∈(2π,3π),求f(x)的单调区间.
考点:三角函数中的恒等变换应用,同角三角函数基本关系的运用
专题:三角函数的图像与性质
分析:化简解析式可得f(x)=1-3
cos(x-
),由x∈(2π,3π),有设t=x-
,t∈(
,
),根据三角函数的单调性即可求f(x)的单调区间.
| 2 |
| π |
| 4 |
| π |
| 4 |
| 7π |
| 4 |
| 11π |
| 4 |
解答:
解:f(x)=cosx(cosx-3)+sinx(sinx-3)
=cos2x-3cosx+sin2x-3sinx
=1-3(cosx+sinx)
=1-3
cos(x-
)
∵x∈(2π,3π),
∴设t=x-
,t∈(
,
),
∵当x∈(2π,3π)时,3
cost在区间t∈(
,
)上是单调递增的,
∴当x∈(2π,3π)时,f(x)的单调递减区间是(
,
).
∵当x∈(2π,3π)时,3
cost在区间t∈(
,
)上是单调递减的,
∴当x∈(2π,3π)时,f(x)的单调递增区间是(
,
).
=cos2x-3cosx+sin2x-3sinx
=1-3(cosx+sinx)
=1-3
| 2 |
| π |
| 4 |
∵x∈(2π,3π),
∴设t=x-
| π |
| 4 |
| 7π |
| 4 |
| 11π |
| 4 |
∵当x∈(2π,3π)时,3
| 2 |
| 7π |
| 4 |
| 9π |
| 4 |
∴当x∈(2π,3π)时,f(x)的单调递减区间是(
| 7π |
| 4 |
| 9π |
| 4 |
∵当x∈(2π,3π)时,3
| 2 |
| 9π |
| 4 |
| 11π |
| 4 |
∴当x∈(2π,3π)时,f(x)的单调递增区间是(
| 9π |
| 4 |
| 11π |
| 4 |
点评:本题主要考查了三角函数中的恒等变换应用,同角三角函数基本关系的运用,三角函数值域的解法,综合性强,属于中档题.

练习册系列答案
相关题目
圆(x+1)2+(y-2)2=1与圆x2+y2=9的位置关系是( )
| A、相交 | B、外切 | C、相离 | D、内切 |
已知θ为三角形的一个内角,且sinθ+cosθ=
,则x2sinθ+y2cosθ=1表示( )
| 1 |
| 4 |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |
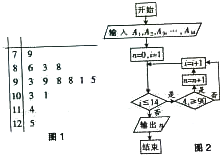 如图是某高三学生14次数学考试成绩的茎叶图(图1),现在将该14个数据依次记为A1,A2,…,A14,并输入如图2所示的一个算法流程图,那么该算法流程图运行结束时输出n的值是( )
如图是某高三学生14次数学考试成绩的茎叶图(图1),现在将该14个数据依次记为A1,A2,…,A14,并输入如图2所示的一个算法流程图,那么该算法流程图运行结束时输出n的值是( )