题目内容
2.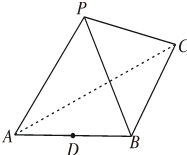 在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.
在三棱锥P-ABC中,△PBC和△PAC是边长为$\sqrt{2}$的等边三角形,AB=2,D是AB中点.(1)在棱PA上求一点M,使得DM∥面PBC;
(2)求证:面PAB⊥面ABC;
(3)求二面角P-BC-A的正弦值.
分析 (1)证明DM∥PB,然后证明DM∥面PBC;
(2)连结CD,PD,证明PD⊥DC,PD⊥AB,说明PD⊥面ABC,然后证明面PAB⊥面ABC;
(3)取BC的中点E,连接DE,PE,说明∠PED是二面角P-BC-A的平面角,然后通过求解三角形即可得到结果.
解答  (1)证明:当M为棱PA中点时,DM∥面PBC,
(1)证明:当M为棱PA中点时,DM∥面PBC,
因为D是AB中点,M是PA的中点,所以DM∥PB,
因为PB?面PBC,DM?面PBC,所以DM∥面PBC;
(2)证明:连结CD,PD,因为$AC=BC=\sqrt{2}$,D为AB中点,AB=2,
所以DC⊥AB,DC=1同理,PD⊥AB,PD=1.
又因为$PC=\sqrt{2}$,则PC2=PD2+DC2,所以∠PDC=90°,即PD⊥DC,
因为PD⊥AB,CD∩AB=D,所以PD⊥面ABC,因为PD?面PAB,
所以面PAB⊥面ABC;
(3)解:取BC的中点E,连接DE,PE,
因为$PB=PC=BC=\sqrt{2}$,所以PE⊥BC,且$PE=\frac{{\sqrt{6}}}{2}$,
因为DC=DB,所以DE⊥BC,则∠PED是二面角P-BC-A的平面角,
因为PD⊥面ABC,所以∠PDE=90°,
故$sin∠PED=\frac{PD}{PE}=\frac{{\sqrt{6}}}{3}$.
点评 本题考查二面角的平面角以及直线与平面平行,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
10.梯形ABCD中,$\overrightarrow{AB}$=λ$\overrightarrow{AD}$+μ$\overrightarrow{BC}$,则λ+μ=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 不能确定 |
17.已知正方体ABCD-A1B1C1D1棱长为1,E、F为线段B1D1的两个动点,且EF=$\frac{\sqrt{2}}{2}$,给出下列四个命题:
①AC⊥BE;
②EF∥平面ABCD;
③点B到平面AEF的距离为定值;
④异面直线AE与BF所成的角为定值.
其中真命题的个数为( )
①AC⊥BE;
②EF∥平面ABCD;
③点B到平面AEF的距离为定值;
④异面直线AE与BF所成的角为定值.
其中真命题的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个. |
7.在四面体ABCD中,已知棱AC的长为$\sqrt{3}$,其余各棱长都为2,则二面角A-BD-C的大小为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
14.曲线$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{25-k}$=1(0<k<9)的关系是( )
| A. | 有相等的焦距,相同的焦点 | B. | 有不同的焦距,不同的焦点 | ||
| C. | 有相等的焦距,不同的焦点 | D. | 以上都不对 |
 在
在 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=$\sqrt{2}$,∠ABC=45°,AE⊥PC,垂足为E. 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形,又PD⊥底面ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.