��Ŀ����
15��ij��ľ��˾ҪΪһС����ֲ3�þ�������ÿ�����ijɱ�Ϊ1000Ԫ���������ijɻ���Ϊ$\frac{2}{3}$���мס������ַ������£�����������һ����ֲ��ȫ���ɻС��ȫ���8000Ԫ������һ��ɻ��ʲ���$\frac{1}{2}$����ֹ������С�������κο�����ɻ��ʳ���$\frac{1}{2}$����û��ȫ�ɻ�ڶ��깫˾����û�гɻ�������֣������ֵ���ȫ���ɻС������8000Ԫ��������ֹ������С��������˾2000Ԫ��
�ҷ�����ֻ��������֤�ɻÿ����С��������˾1300Ԫ��
��1����ʵ�м�������С������ľ��˾����ĸ��ʣ�
��2����˾Ϊ��ø�������Ӧѡ�����ַ�����
���� ��1����С������Ϊ�¼�A������n���ظ��������¼�Aǡ�÷���k�εĸ��ʼ��㹫ʽ�����С������ľ��˾����ĸ��ʣ�
��2�������������ο���ȡֵΪ��-3��-2��4��5���ֱ������Ӧ�ĸ��ʣ��ɴ�������ε���ѧ������������ҷ��������Ӷ��õ���ľ��˾ѡ�ü���������ľ�ֵ����
��� �⣺��1����С������Ϊ�¼�A��
��$P��A��=C_3^2{��\frac{2}{3}��^2}\frac{1}{3}+{��\frac{2}{3}��^3}=\frac{20}{27}$��
����С������ľ��˾����ĸ���Ϊ$\frac{20}{27}$������5�֣�
��2�������������ο���ȡֵΪ��-3��-2��4��5������6�֣�
$P����=-3��=C_3^1{��\frac{1}{3}��^2}\frac{2}{3}+{��\frac{1}{3}��^3}=\frac{7}{27}$��
$P����=-2��=C_3^2{��\frac{2}{3}��^2}\frac{1}{3}•\frac{1}{3}=\frac{4}{27}$��
$P����=4��=C_3^2{��\frac{2}{3}��^2}\frac{1}{3}•\frac{2}{3}=\frac{8}{27}$��
$P����=5��={��\frac{2}{3}��^3}=\frac{8}{27}$��
��εķֲ���Ϊ��
| �� | -3 | -2 | 4 | 5 |
| P | $\frac{7}{27}$ | $\frac{4}{27}$ | $\frac{8}{27}$ | $\frac{8}{27}$ |
�ҷ���������0.9ǧԪ��
��0.9$��\frac{43}{27}$������ľ��˾ѡ�ü���������ľ�ֵ������12�֣�
���� ���⿼����ʵ���������ɢ����������ķֲ��м���ѧ��������Ӧ�ã����е��⣬������߿��ж��DZؿ�����֮һ��

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�| A�� | 4 | B�� | 3 | C�� | -5 | D�� | 5 |
| A�� | an+1=an+n��n��N* | B�� | an=an-1+n��n��N*��n��2 | ||
| C�� | an+1=an+��n+1����n��N*��n��2 | D�� | an=an-1+��n-1����n��N*��n��2 |
| A�� | $\frac{��}{2}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{��}{4}$ | D�� | $\frac{��}{6}$ |
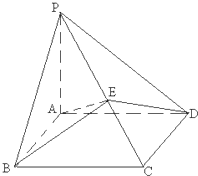 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD���ı���ABCDΪƽ���ı��Σ�AB=1��BC=$\sqrt{2}$����ABC=45�㣬AE��PC������ΪE��
��ͼ��������P-ABCD�У�PA��ƽ��ABCD���ı���ABCDΪƽ���ı��Σ�AB=1��BC=$\sqrt{2}$����ABC=45�㣬AE��PC������ΪE�� ���ⳤΪ2��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪA1B1��CD���е㣮
���ⳤΪ2��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪA1B1��CD���е㣮