题目内容
16.对于R上可导的任意函数f(x),若满足f(x)=f(2-x),且(x-1)f′(x)≥0,则必有( )| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
分析 由(x-1)f′(x)≥0,可得x>1时,f′(x)≥0,此时函数f(x)单调递增;x<1时,f′(x)≤0,此时函数f(x)单调递减.l利用单调性即可判断出结论.
解答 解:由(x-1)f′(x)≥0,可得x>1时,f′(x)≥0,此时函数f(x)单调递增;
x<1时,f′(x)≤0,此时函数f(x)单调递减.
∵满足f(x)=f(2-x),∴函数f(x)关于直线x=1对称,
∴f(0)≥f(1),f(2)≥f(1),
∴f(0)+f(2)≥2f(1),
故选:C.
点评 本题考查了利用导数研究函数的单调性,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.在四面体ABCD中,已知棱AC的长为$\sqrt{3}$,其余各棱长都为2,则二面角A-BD-C的大小为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
8.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,则异面直线BC1与AC所成角的余弦值为( )
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{1}{2}$ |
 在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.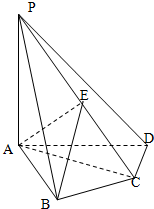 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.