题目内容
2．定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，则符合条件$|\begin{array}{l}{z}&{1+i}\\{2}&{1}\end{array}|$=0的复数z对应的点在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 直接利用新定义得到关于z的等式，求得z后得答案．
解答 解：由题意可得，|$|\begin{array}{l}{z，}&{1+i}\\{2，}&{1}\end{array}|$|=z-2（1+i）=0，
则z=2+2i，
∴复数z对应的点的坐标为（2，2），在第一象限．
故选：A．
点评 本题是新定义题，考查复数的代数表示法及其几何意义，是基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10．在伸缩变换$\left\{\begin{array}{l}{x′=3x}\\{y′=y}\end{array}\right.$的作用后，点（1，2）的坐标变为（ ）
| A． | （3，2） | B． | （1，2） | C． | （$\frac{1}{3}$，2） | D． | （1，$\frac{2}{3}$） |
7．定义运算$|\begin{array}{l}{a，}&{b}\\{c，}&{d}\end{array}|$=ad-bc，则符合条件$|\begin{array}{l}{z，}&{1+i}\\{-i，}&{2i}\end{array}|$=0的复数$\overline{z}$对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | C第三象限 | D． | 第四象限 |
12．设等比数列{an}的前n项和为Sn，若a2=3，且a2015+a2016=0，则S101等于（ ）
| A． | 3 | B． | 303 | C． | -3 | D． | -303 |
8．已知实数x，y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{4x-y-4≤0}\\{\;}\end{array}\right.$，则当3x-y取得最小值时，$\frac{x-5}{y+3}$的值为（ ）
| A． | -$\frac{2}{3}$ | B． | $\frac{2}{3}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
9．
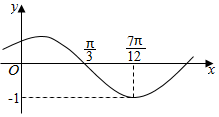已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，将函数f（x）的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，将函数f（x）的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin（2x-$\frac{π}{3}$） | B． | g（x）=sin（2x+$\frac{π}{6}$） | C． | g（x）=-sin（2x-$\frac{π}{3}$） | D． | g（x）=sin（4x+$\frac{π}{6}$） |