题目内容
17．设集合{$\frac{3}{a}$+b|1≤a≤b≤2}中的最大和最小元素分别是M、m，则M=5，m=2$\sqrt{3}$．分析 根据级别不等式的性质求出最小值，a取最小值1，b取最大值2时，求出最大值M．
解答 解：$\frac{3}{a}$+b≥$\frac{3}{a}$+a≥2$\sqrt{3}$，故m=2$\sqrt{3}$，
a=1，b=2时$\frac{3}{a}$+b=5，故M=5，
故答案为：$5，2\sqrt{3}$．
点评 本题考查了集合问题，考查级别不等式的性质，是一道基础题．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12．下列函数在其定义域内既是奇函数又是增函数的是（ ）
| A． | y=2-x | B． | y=x3+x | C． | y=-$\frac{1}{x}$ | D． | y=lnx |
2．定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，则符合条件$|\begin{array}{l}{z}&{1+i}\\{2}&{1}\end{array}|$=0的复数z对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
9．将函数f（x）=sin（2x-$\frac{π}{2}$）的图象向右平移$\frac{π}{4}$个单位后得到函数g（x），则g（x）具有性质（ ）
| A． | 最大值为1，图象关于直线x=$\frac{π}{2}$对称 | B． | 在（0，$\frac{π}{4}$）上单调递减，为奇函数 | ||
| C． | 在（-$\frac{3π}{8}$，$\frac{π}{8}$）上单调递增，为偶函数 | D． | 周期为π，图象关于点（$\frac{3π}{8}$，0）对称 |
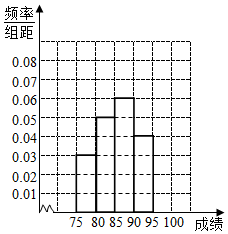将某校高三年级300名学生的毕业会考数学成绩进行整理后，分成五组，第-组[75，80），第二组[80，85），第三组[86，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分．