题目内容
8．已知实数x，y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{4x-y-4≤0}\\{\;}\end{array}\right.$，则当3x-y取得最小值时，$\frac{x-5}{y+3}$的值为（ ）| A． | -$\frac{2}{3}$ | B． | $\frac{2}{3}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
分析 先画出满足条件的平面区域，求出2x-y取得最小值时A点的坐标，将A点的坐标代入$\frac{x-5}{y+3}$，求解即可．
解答 解：满足条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{4x-y-4≤0}\\{\;}\end{array}\right.$的平面区域，如图，
令z=3x-y，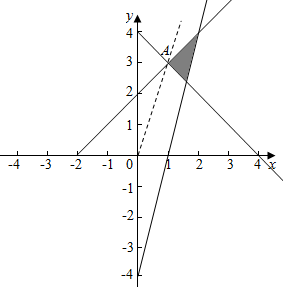
则当直线z=3x-y经过直线x-y+2=0和直线
x+y-4=0的交点A时，z取得最小值．
此时A的坐标为（1，3），
∴$\frac{x-5}{y+3}$=$-\frac{2}{3}$
故选：A．
点评 本题考察了简单的线性规划问题，考察数形结合思想，求出2x-y取得最小值时的x，y的值是解题的关键，本题是一道中档题．
练习册系列答案
相关题目
1．某银行在我市举行了“网上银行、手机银行办理业务免费政策”满意度测评，共有10000人参加了这次测评（满分100分，得分全为整数），为了解本次测评分数情况，从中随机抽取了部分人的测评分数进行统计，整理见如表：
（1）求出表中a，b，c的值；
（2）若分数字80（含80分）以上表示对“网上银行、手机银行办理业务免费政策”非常满意，其中分数在90（含有90分）以上表示“十分满意”，现从被抽取的“”非常满意人群中随机抽取2人，求至少一人分数是“十分满意”的概率；
（3）请你根据样本数据估计全市的平均测评分数．
| 组别 | 分组 | 频数 | 频率 |
| 1 | [50，60） | a | 0.08 |
| 2 | [60，70） | 15 | 0.3 |
| 3 | [70，80） | 21 | c |
| 4 | [80，90） | 6 | 0.12 |
| 5 | [90，100） | 4 | 0.08 |
| 合计 | b | 1.00 | |
（2）若分数字80（含80分）以上表示对“网上银行、手机银行办理业务免费政策”非常满意，其中分数在90（含有90分）以上表示“十分满意”，现从被抽取的“”非常满意人群中随机抽取2人，求至少一人分数是“十分满意”的概率；
（3）请你根据样本数据估计全市的平均测评分数．
2．定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，则符合条件$|\begin{array}{l}{z}&{1+i}\\{2}&{1}\end{array}|$=0的复数z对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
如图，在△ABC中，C=$\frac{π}{3}$，BC=4，点D在边AC上，AD=DB，DE⊥AB，E为垂足，若DE=2$\sqrt{2}$，求cosA=$\frac{\sqrt{6}}{4}$．