题目内容
抛物线x2=4y的准线l与y轴交于点P,若l绕点P以每秒
弧度的角速度按逆时针方向旋转t1秒后,恰好与抛物线第一次相交于一点,再旋转t2秒后,恰好与抛物线第二次相相交于一点,则t2的值为( )
| π |
| 12 |
| A、6 | B、4 | C、3 | D、2 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据抛物线的方程,找出p的值,进而得到其准线方程和P的坐标,根据直线l过P点,设出直线l的斜率为k时与抛物线相切,表示出此时直线l的方程,与抛物线联立,消去y得到关于x的一元二次方程,令根的判别式等于0列出关于k的方程,求出方程的解即可得到k的值,从而确定出直线l的倾斜角,用求出的倾斜角除以角速度即可求出此时所用的时间t1=3.同理,旋转t2秒后,恰好与抛物线第二次相相交于一点,则t2=3.
解答:
解:根据抛物线的方程x2=4y,得到p=1,
所以此抛物线的准线方程为y=-1,P坐标为(0,-1),
令恒过P点的直线y=kx-1与抛物线相切,
联立直线与抛物线,消去y得:x2-4kx+4=0,得到△=k2-1=0,即k2=1,
解得:k=1或k=-1,
由直线l绕点P逆时针旋转,k=-1不合题意,舍去,
则k=1,此时直线的倾斜角为
又P的角速度为每秒
弧度,
所以直线l恰与抛物线第一次相切,则t1=3.
同理,旋转t2秒后,恰好与抛物线第二次相相交于一点,则t2=3,
故选C.
所以此抛物线的准线方程为y=-1,P坐标为(0,-1),
令恒过P点的直线y=kx-1与抛物线相切,
联立直线与抛物线,消去y得:x2-4kx+4=0,得到△=k2-1=0,即k2=1,
解得:k=1或k=-1,
由直线l绕点P逆时针旋转,k=-1不合题意,舍去,
则k=1,此时直线的倾斜角为
| π |
| 4 |
| π |
| 12 |
所以直线l恰与抛物线第一次相切,则t1=3.
同理,旋转t2秒后,恰好与抛物线第二次相相交于一点,则t2=3,
故选C.
点评:本题以抛物线为载体,考查抛物线的简单性质,直线与曲线相切位置关系的应用,解题的一般式步骤是;设出直线的方程,联立直线与曲线方程,整理可得一元二次方程,方程判别式等于0,求解参数的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知点A(0,1),B(-2,3)C(-1,2),D(1,5),则向量
在
方向上的投影为( )
| AC |
| BD |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设f(x)=x(x-1)(x-2)…(x-2015),则f′(2015)=( )
| A、-2013! |
| B、-2015! |
| C、2013! |
| D、2015! |
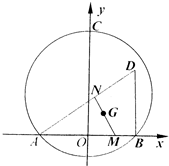 在平面直角坐标系xOy中,已知点A(-1,0),B(1,0),C(0,a)(a∈R且a≠0),且动点D满足DA=
在平面直角坐标系xOy中,已知点A(-1,0),B(1,0),C(0,a)(a∈R且a≠0),且动点D满足DA=