已知2＜${∫} {2}^{3}$(k+2)dx＜4.则实数k的取值范围为(0.2)．题目和参考答案——青夏教育精英家教网—

题目内容

15．已知2＜${∫}_{2}^{3}$（k+2）dx＜4，则实数k的取值范围为（0，2）．

分析先利用积分定理求出${∫}_{2}^{3}$（k+2）dx，然后解不等式即可求解k的范围．

解答解：因为2＜${∫}_{2}^{3}$（k+2）dx＜4，${∫}_{2}^{3}$（k+2）dx=（k+2）x|${\;}_{2}^{3}$=k+2，所以2＜k+2＜4，解得0＜k＜2；
故答案为：（0，2）

点评本题主要考查了定积分定理的简单应用，属于基础题．

练习册系列答案

6．已知x，y满足$\left\{\begin{array}{l}y≥-1\\ x+y≤1\\ y≤x\end{array}\right.$，则z=2x+y的最小值是（　　）

3．已知全集U={1，2，3，4，5，6，7}，集合A={2，4，5}，B={1，3，5，7}，则（∁_UA）∩B={1，3，7}．

10．已知函数y=f（x）的导函数y=f′（x）的图象如图所示，则关于函数y=f（x），下列说法正确的是（　　）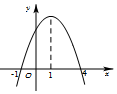

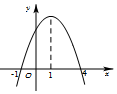
	A．	在x=-1处取得极大值		B．	在区间[-1，4]上是增函数
	C．	在x=1处取得极大值		D．	在区间[1，+∞）上是减函数

20．圆ρ=$\sqrt{2}$（cosθ+sinθ）的圆心极坐标是（1，$\frac{π}{4}$）．

7．为了加强某站的安全检查，从甲乙丙等5名候选民警中选2名作为安保人员，则甲乙丙中有2人被选中的概率为（　　）

4．在区间（0，+∞）内，函数f（x）=e^x-x是（　　）

5．双曲线x²-my²=1（m∈R）的右焦点坐标为（2，0），则该双曲线的渐近线方程为（　　）

A．

y=±$\sqrt{3}$x

B．

y=$±\frac{\sqrt{3}}{3}$

试题分类