题目内容
已知双曲线的焦点在x轴上，两个顶点间的距离为2，焦点到渐近线的距离为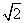
.
(1) 求双曲线的标准方程；
(2) 写出双曲线的实轴长、虚轴长、焦点坐标、离心率、渐近线方程．
解：(1) 依题意可设双曲线的方程为
＝1(a>0, b>0)，则2a＝2, 所以a＝1.设双曲线的一个焦点为(c, 0), 一条渐近线的方程为bx－ ay ＝ 0，则焦点到渐近线的距离d＝
＝b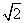＝，所以双曲线的方程为x2－
＝1.
(2) 双曲线的实轴长为2，虚轴长为2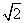，焦点坐标为(－
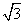， 0), (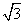， 0)，离心率为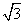，渐近线方程为y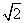＝±x.
练习册系列答案
优学名师名题系列答案
相关题目
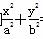＝1(a>b>0)，F1、F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B.
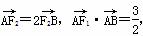，求椭圆的方程．
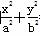＝1(a>b>0)的离心率为
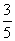，且过点P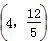
，A为上顶点，F为右焦点．点Q(0，t)是线段OA(除端点外)上的一个动点，过Q作平行于x轴的直线交直线AP于点M，以QM为直径的圆的圆心为N.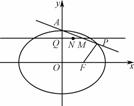
－y2＝1的一个焦点为(2，0)，则它的离心率为________．
＝1的离心率e＝2，则m＝________．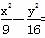
＝1有共同的渐近线，且过点(－3，2
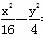＝1有公共焦点，且过点(3
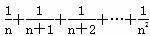＞1(n∈N*且n＞1)．