题目内容
已知椭圆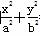 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为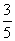 ,且过点P
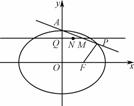
,且过点P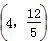 ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
(1) 求椭圆方程;
(2) 若圆N与x轴相切,求圆N的方程;
(3) 设点R为圆N上的动点,点R到直线PF的最大距离为d,求d的取值范围.
解:(1) ∵ e=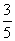 ,不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为
,不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为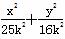 =1(a>b>0),∵ P
=1(a>b>0),∵ P 在椭圆上,∴
在椭圆上,∴ 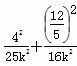 =1,解得k=1,
=1,解得k=1,
∴ 椭圆方程为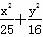 =1.
=1.
(2) kAP=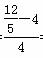 =-
=-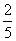 ,则直线AP的方程为y=-
,则直线AP的方程为y=-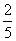 x+4,令y=t(0<t<4),则x=
x+4,令y=t(0<t<4),则x=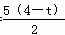 ,∴ M
,∴ M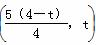 ,
,
∵ Q(0,t),∴ N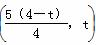 ,
,
∵ 圆N与x轴相切,∴ 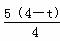 =t,由题意M为第一象限的点,则
=t,由题意M为第一象限的点,则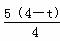 =t,解得t=
=t,解得t=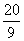 ,
,
∴ N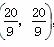 ,
,
圆N的方程为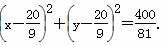
(3) F(3,0),kPF=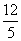 ,
,
∴ 直线PF的方程为y=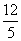 (x-3),即12x-5y-36=0,
(x-3),即12x-5y-36=0,
∴ 点N到直线PF的距离为
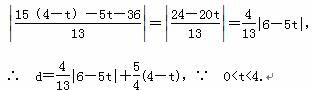
∴ 当0<t≤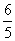 时,d=
时,d=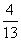 (6-5t)+
(6-5t)+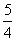 (4-t)=
(4-t)=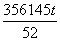 ,此时
,此时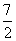 ≤d<
≤d<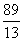 ;
;
当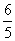 <t<4时,d=
<t<4时,d=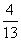 (5t-6)+
(5t-6)+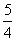 (4-t)=
(4-t)=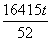 ,此时
,此时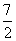 <d<
<d<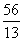 .
.
∴ 综上,d的取值范围为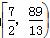 .
.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

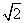 .
.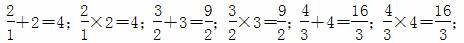 …,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.
…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.