题目内容
已知函数f(x)=mx2-mx-1
(1)若2是方程f(x)=
x的一个根,an=
(n∈N*),求数列{an}的前n项和Sn
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.
(1)若2是方程f(x)=
| 1 |
| 2 |
f(n)+
|
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.
考点:数列与函数的综合,函数恒成立问题
专题:等差数列与等比数列
分析:(1)通过2是方程f(x)=
x的一个根,求出m,化简an=
(n∈N*),利用等差数列求数列{an}的前n项和Sn
(2)利用对于x∈[1,3],f(x)<5-m恒成立,得到m的不等式,利用二次函数闭区间上的最值,求实数m的取值范围.
| 1 |
| 2 |
f(n)+
|
(2)利用对于x∈[1,3],f(x)<5-m恒成立,得到m的不等式,利用二次函数闭区间上的最值,求实数m的取值范围.
解答:
解:(1)由题意2是方程f(x)=
x的一个根,可得4m-2m-1=1,
解得m=1,∵an=
(n∈N*),
∴an=n-
,
∴Sn=
=
(6分)
(2)∵f(x)<-m+5?m(x2-x+1)<6,
∵x2-x+1>0,∴m<
,
对于x∈[1,3]恒成立,记g(x)=
,x∈[1,3],
记h(x)=x2-x+1,h(x)在x∈[1,3]上为增函数.则g(x)在[1,3]上为减函数,
∴[g(x)]min=g(3)=
,∴m<
.所以m的取值范围为(-∞,
).(12分)
| 1 |
| 2 |
解得m=1,∵an=
f(n)+
|
∴an=n-
| 1 |
| 2 |
∴Sn=
n(
| ||||
| 2 |
| n2 |
| 2 |
(2)∵f(x)<-m+5?m(x2-x+1)<6,
∵x2-x+1>0,∴m<
| 6 |
| x2-x+1 |
对于x∈[1,3]恒成立,记g(x)=
| 6 |
| x2-x+1 |
记h(x)=x2-x+1,h(x)在x∈[1,3]上为增函数.则g(x)在[1,3]上为减函数,
∴[g(x)]min=g(3)=
| 6 |
| 7 |
| 6 |
| 7 |
| 6 |
| 7 |
点评:本题考查数列与函数结合,函数的最值以及函数的恒成立,构造法的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
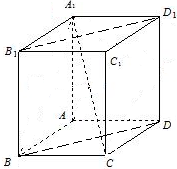 已知长方体A1B1C1D1-ABCD的高为
已知长方体A1B1C1D1-ABCD的高为