题目内容
5. 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 取BD的中点O,连接AO,EO,C′O,可得∠AOE=45°,∠EOC′=30°,∠OC′E=∠OAE,由正弦定理能求出$\frac{AE}{EC′}$的值.
解答 解:取BD的中点O,连接AO,EO,C′O,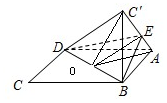
∵菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,
∴C′O⊥BD,AO⊥BD,OC′=OA,
∴BD⊥平面AOC′,
∴EO⊥BD,
∵二面角A-BD-E与二面角E-BD-C′的大小分别为45°和30°,
∴∠AOE=45°,∠EOC′=30°,
∵OC′=OA,∴∠OC′E=∠OAE,
由正弦定理得$\frac{OE}{sin∠OC′E}$=$\frac{EC′}{sin∠EOC′}$,$\frac{OE}{sin∠OAE}=\frac{AE}{sin∠AOE}$,
∴$\frac{EC′}{sin∠EOC′}=\frac{AE}{sin∠AOE′}$,
∴$\frac{AE}{EC′}=\frac{sin45°}{sin30°}=\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}=\sqrt{2}$.
故选:D.
点评 本题考查二面角的平面角及其求法,考查空间想象能力和思维能力,训练了正弦定理在求解三角形问题中的应用,是中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
15.已知正方形ABCD的边长为1,若在正方形内(包括边界)任取一点M,则△ABM的面积不小于$\frac{1}{8}$的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
13.已知f(x)=x3-$\frac{9}{2}$x2+6x-a,若对任意的x,f′(x)≥m恒成立,则m的最大值为( )
| A. | 3 | B. | 2 | C. | 1 | D. | -$\frac{3}{4}$ |
15. 如图所示的程序框图中输入x的值是[1,9]内任取的一个实数,执行该程序,则输出x的值小于55的概率为( )
如图所示的程序框图中输入x的值是[1,9]内任取的一个实数,执行该程序,则输出x的值小于55的概率为( )
 如图所示的程序框图中输入x的值是[1,9]内任取的一个实数,执行该程序,则输出x的值小于55的概率为( )
如图所示的程序框图中输入x的值是[1,9]内任取的一个实数,执行该程序,则输出x的值小于55的概率为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |