题目内容
已知f（x）=2sin（2x+
），x∈R．
（1）求f（x）的最小正周期、单调区间和对称轴．
（2）当x∈[-
，
]时，求f（x）值域．
| π |
| 6 |
（1）求f（x）的最小正周期、单调区间和对称轴．
（2）当x∈[-
| π |
| 4 |
| π |
| 4 |
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（1）根据f（x）=2sin（2x+
），x∈R，可得它的周期，再根据正弦函数的单调区间求得f（x）的单调区间．
（2）根据x∈[-
，
]，利用正弦函数的定义域和值域求得函数的值域．
| π |
| 6 |
（2）根据x∈[-
| π |
| 4 |
| π |
| 4 |
解答：
解：（1）由于f（x）=2sin（2x+
），x∈R，故它的周期为
=π，
令2kπ-
≤2x+
≤2kπ+
，k∈z，求得 kπ-
≤x≤kπ+
，
可得函数的增区间为[kπ-
≤x≤kπ+
]，k∈z．
令2kπ+
≤2x+
≤2kπ+
，k∈z，求得 kπ+
≤x≤kπ+
，
可得函数的减区间为[kπ+
≤x≤kπ+
]，k∈z．
（2）当x∈[-
，
]时，2x+
∈[-
，
]，∴当2x+
=-
时，函数取得最小值为-
，
当2x+
=
时，函数取得最大值为2，
故函数的值域为[-
，2]．
| π |
| 6 |
| 2π |
| 2 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
可得函数的增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
令2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
可得函数的减区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
（2）当x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 3 |
当2x+
| π |
| 6 |
| π |
| 2 |
故函数的值域为[-
| 3 |
点评：本题主要考查正弦函数的周期性、单调性、定义域和值域，属于基础题．
练习册系列答案
相关题目
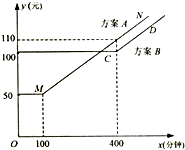移动公司根据市场客户的不同需求，对某地区的手机套餐通话费提出两种优惠方案，两种方案所付电话费（元）与通话时间（分钟）之间的关系如图所示（实线部分：MN与CD平行即直线方程y=kx+b中的斜率k相等）．
如图，已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中，AC=3，AB=5，BC=4，AA1=4，点D是AB的中点．