题目内容
若函数y＝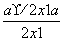
为奇函数．
(1)求a的值；
(2)求函数的定义域；
(3)求函数的值域．
解析 ∵函数y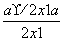＝，∴y＝a－
.
(1)由奇函数的定义，可得f(－x)＋f(x)＝0，即
a－＋a－＝0，
∴2a＋
＝0，∴a＝－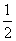
.
(2)∵y＝－－，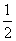
∴2x－1≠0，即x≠0.
∴函数y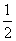＝－－的定义域为{x|x≠0}．
(3)∵x≠0，∴2x－1＞－1.
∵2x －1≠0，∴0＞2x－1＞－1或2x－1＞0.
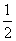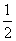∴－－＞或－－＜－.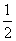
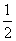即函数的值域为{y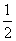|y＞或y＜－}．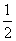
练习册系列答案
名校课堂系列答案
相关题目
已知函数f(x)、g(x)分别由下表给出：
| x | 1 | 2 | 3 |
| f(x) | 1 | 3 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
则f[g(1)]的值为________；满足f[g(x)]>g[f(x)]的x的值是________．
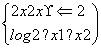则f(f(5))＝( )．
的图象（ ）