题目内容
12.已知动点P到y轴的距离比它到点M(-1,0)的距离少1.(1)求动点P的轨迹方程;
(2)若直线l:x+y+1=0与动点P的轨迹交于A、B两点,求△OAB的面积.
分析 (1)设出P的坐标,由题意列式,对x分类化简得答案;
(2)联立直线方程与抛物线方程,化为关于x的一元二次方程,利用根与系数的关系及抛物线的焦点弦长公式求得|AB|,再由点到直线的距离公式求出O到直线AB的距离,代入三角形面积公式得答案.
解答 解:(1)设P(x,y),则|x|+1=$\sqrt{(x+1)^{2}+{y}^{2}}$.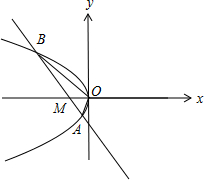
若x>0,则x+1=$\sqrt{(x+1)^{2}+{y}^{2}}$,两边平方并整理得y=0;
若x<0,则1-x=$\sqrt{(x+1)^{2}+{y}^{2}}$,两边平方并整理得y2=-4x.
∴P点轨迹方程为y=0(x>0)或y2=-4x;
(2)设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y^2}=-4x\\ x+y+1=0\end{array}\right.$,消去y得:x2+6x+1=0.
则x1+x2=-6,
∴|AB|=2-(x1+x2)=8,
原点O到直线x+y+1=0的距离d=$\frac{|1|}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
∴${S}_{△AOB}=\frac{1}{2}×8×\frac{\sqrt{2}}{2}=2\sqrt{2}$.
点评 本题考查轨迹方程的求法,考查了直线与抛物线位置关系的应用,是中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
2.下列各组对象不能组成集合的是( )
| A. | 里约热内卢奥运会的比赛项目 | B. | 中国文学四大名著 | ||
| C. | 我国的直辖市 | D. | 抗日战争中著名的民族英雄 |
4.过点(0,0)且倾斜角为60°的直线的方程是( )
| A. | $\sqrt{3}$x+y=0 | B. | $\sqrt{3}$x-y=0 | C. | x+$\sqrt{3}$y=0 | D. | x-$\sqrt{3}$y=0 |
1.在△ABC中,∠C=90°,0°<A<45°,则下列各式中,正确的是( )
| A. | sinA>sinB | B. | tanA>tanB | C. | cosA<sinA | D. | cosB<sinB |