题目内容
3.(1)从装有3个红球、2个白球的袋中任取3个球,求所取的3个球中至少有1个白球的概率?(2)在半径为1的圆中随机地撒一大把豆子,求豆子落在圆内接正方形中的概率?
分析 (1)用间接法,首先分析从5个球中任取3个球的情况数,再求出所取的3个球中没有白球,即全部是红球的情况数,计算没有白球的概率,而“没有白球”与“3个球中至少有1个白球”为对立事件,由对立事件的概率公式可得答案;
(2)根据题意画出图形,由正方形面积除以圆面积求概率.
解答 解:(1)根据题意,求得从5个球中任取3个球,共C53=10种取法,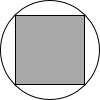
所取的3个球中没有白球即全部红球的情况有C33=1种,
则没有白球的概率为$\frac{1}{10}$,
则所取的3个球中至少有1个白球的概率是1-$\frac{1}{10}$=$\frac{9}{10}$;
(2)如图,
∵圆的半径为1,则直径为2,∴正方形边长为$\sqrt{2}$,
则豆子落在圆内接正方形中的概率P=$\frac{(\sqrt{2})^{2}}{π•{1}^{2}}=\frac{2}{π}$.
点评 本题考查古典概型概率的求法,注意至多、至少一类的问题,可以选用间接法,即借助对立事件的概率的性质,先求其对立事件的概率,进而求出其本身的概率,对于几何概型,解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=$\frac{N(A)}{N}$求解,是基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
13.已知角α终边上一点P(-2,3),则$\frac{cos(\frac{π}{2}+α)sin(π+α)}{cos(π-α)sin(3π-α)}$的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
14.设 α为锐角,$\overrightarrow a=(sinα,1)$,$\overrightarrow b=(1,2)$,若$\overrightarrow a$与$\overrightarrow b$共线,则角α=( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
8.若数列{an}的通项公式是an=(-1)n(3n-1),前n项和为Sn,则S11等于( )
| A. | -187 | B. | -2 | C. | -32 | D. | -17 |
13.三个好朋友同时考进同一所高中,该校高一有10个班级,则至少有2人分在同一个班级的概率为( )
| A. | $\frac{7}{25}$ | B. | $\frac{18}{25}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |