题目内容
20.若椭圆9x2+25y2=225上一点M到焦点F1的距离为2,N是MF1的中点,O为坐标原点,则ON=4.分析 利用椭圆的定义可得|MF2|,再利用三角形中位线定理即可得出.
解答  解:椭圆9x2+25y2=225化为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1,
解:椭圆9x2+25y2=225化为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1,
可得a=5,
∴|MF1|+|MF2|=2a=10,
又|MF1|=2,
∴|MF2|=8,
∵N是MF1的中点,O为F1F2的中点,
∴|ON|=$\frac{1}{2}|M{F}_{2}|$=4.
故答案为:4.
点评 本题考查了椭圆的定义标准方程及其性质、三角形中位线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知i为虚数单位,复数z=$\frac{1-2i}{a+i}$的实部与虚部互为相反数,则实数a=( )
| A. | -1 | B. | 1 | C. | 3 | D. | -3 |
15.下列函数中值域为实数集的偶函数是( )
| A. | f(x)=|lnx|(x>0) | B. | f(x)=ln|x|(x≠0) | C. | f(x)=x-$\frac{1}{x}$(x≠0) | D. | f(x)=x+$\frac{1}{x}$(x≠0) |
5.已知数列{an}为正项等差数列,满足$\frac{1}{{a}_{1}}$+$\frac{4}{{a}_{2k-1}}$≤1(其中k∈N*,且k≥2),则ak的最小值为$\frac{9}{2}$.
10.设集合A={(x,y)|x2+y2=16,x∈Z,y∈Z},则集合A的子集个数为( )
| A. | 8 | B. | 32 | C. | 16 | D. | 15 |
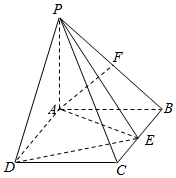 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.