题目内容
16．水平放置的矩形ABCD，长AB=4，宽BC=2，以AB、AD为轴作出斜二测直观图A′B′C′D′，则四边形A′B′C′D′的面积为（ ）| A． | 4$\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 4 | D． | 2 |
分析 根据斜二测画法所得的直观图是一个四边形，它的面积与水平放置的正方形的面积之比的关系，求解即可．
解答 解：水平放置的正方形的面积与斜二测画法所得的直观图是一个四边形，两者面积之比为2$\sqrt{2}$，
所以这个四边形的面积为：4×2×$\frac{1}{2\sqrt{2}}$=2$\sqrt{2}$．
故选：B
点评 本题是基础题，考查斜二测画法与水平放置的平面图形的面积之比问题，牢记基本结论：2$\sqrt{2}$的关系，解题能够提高速度
练习册系列答案
初中暑期衔接系列答案
相关题目
6．当且仅当 ，x2＞2x＞log2x．（ ）
| A． | 3＜x＜4 | B． | x＞4 | C． | 0＜x＜2 | D． | 2＜x＜4 |
8．
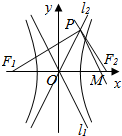已知F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左、右焦点，l1，l2为双曲线的两条渐近线．设过点M（b，0）且平行于l1的直线交l2于点P．若PF1⊥PF2，则该双曲线的离心率为（ ）
已知F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左、右焦点，l1，l2为双曲线的两条渐近线．设过点M（b，0）且平行于l1的直线交l2于点P．若PF1⊥PF2，则该双曲线的离心率为（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\frac{\sqrt{14-2\sqrt{41}}}{2}$ | D． | $\frac{\sqrt{14+2\sqrt{41}}}{2}$ |