题目内容
设各项均为正数的数列{an}的前n项和为Sn,已知2a2=a1+a3,数列
是公差为1的等差数列.数列{bn}满足:bn=
,bn+1=
bn.求数列{an},{bn}的通项公式及前n项和.
| sn |
| 1 |
| 2 |
| n+1 |
| 2n |
考点:等差数列的性质
专题:综合题,等差数列与等比数列
分析:根据等差数列的通项公式,结合已知,列出关于a1、d的方程,求出a1,进而推出Sn,再利用an与Sn的关系求出an.
设bn=ncn(n∈N*).根据等比数列的定义证明数列{cn}是等比数列,首项为
,公比为
,即可求等比数列的通项公式,可得bn=ncn=
,利用“错位相减法”即可得到Tn.
设bn=ncn(n∈N*).根据等比数列的定义证明数列{cn}是等比数列,首项为
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2n |
解答:
解:由题意知:d>0,
=
+(n-1)d,
∵2a2=a1+a3,
∴3a2=S3,即3(S2-S1)=S3,
∴3[(
+d)2-a1]=(
+2d)2,
化简,得:
=d,
∴
=nd,Sn=n2d2,
当n≥2时,an=Sn-Sn-1=n2d2-(n-1)2d2=(2n-1)d2,适合n=1情形.
故所求an=(2n-1)d2.
设bn=ncn(n∈N*).
由bn+1=
bn,可得
=
.
∴数列{cn}是等比数列,首项为
,公比为
,
∴cn=
.
∴bn=ncn=
.
∴Tn=
+
+…+
,
Tn=
+
+…+
,
∴
Tn=
+
+…+
-
=1-
-
,
∴Tn=2-
.
| Sn |
| a1 |
∵2a2=a1+a3,
∴3a2=S3,即3(S2-S1)=S3,
∴3[(
| a1 |
| a1 |
化简,得:
| a1 |
∴
| Sn |
当n≥2时,an=Sn-Sn-1=n2d2-(n-1)2d2=(2n-1)d2,适合n=1情形.
故所求an=(2n-1)d2.
设bn=ncn(n∈N*).
由bn+1=
| n+1 |
| 2n |
| cn+1 |
| cn |
| 1 |
| 2 |
∴数列{cn}是等比数列,首项为
| 1 |
| 2 |
| 1 |
| 2 |
∴cn=
| 1 |
| 2n |
∴bn=ncn=
| n |
| 2n |
∴Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| n |
| 2n+1 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=2-
| 2+n |
| 2n |
点评:本小题主要考查等差数列的通项、求和;考查等比数列的通项公式及其前n项和公式、“错位相减法”等基础知识与基本技能方法,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
已知角α的顶点为坐标原点,始边为x轴正半轴,终边经过点(-4,3),则cosα=( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知集合A={x|x≤1},B={x|x2-2x<0}.则A∩B=( )
| A、(0,1] |
| B、[1,2) |
| C、(0,1) |
| D、(0,2) |
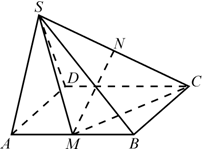 四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.