题目内容
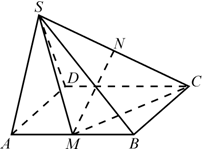 四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求二面角S-CM-D的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取SD的中点R,连结AR、RN,由已知得四边形AMNR是平行四边形,从而MN∥AR,由此能证明MN∥平面SAD.
(Ⅱ)向量法:取AD的中点O,连结OS,过O作AD的垂线交BC于G,分别以OA,OG,OS为x,y,z轴,建立坐标系,利用向量法能求出二面角S-CM-D的余弦值.
几何法:取AD的中点O,连结OS、OB,OB∩CM=H,连结SH,则∠SHO是二面角S-CM-D的平面角,由此能求出二面角S-CM-D的余弦值.
(Ⅱ)向量法:取AD的中点O,连结OS,过O作AD的垂线交BC于G,分别以OA,OG,OS为x,y,z轴,建立坐标系,利用向量法能求出二面角S-CM-D的余弦值.
几何法:取AD的中点O,连结OS、OB,OB∩CM=H,连结SH,则∠SHO是二面角S-CM-D的平面角,由此能求出二面角S-CM-D的余弦值.
解答:
(本小题满分12分)
解:(Ⅰ)如图,取SD的中点R,连结AR、RN,
则RN∥CD,且RN=
CD,AM∥CD,
所以RN∥AM,且RN=AM,
所以四边形AMNR是平行四边形,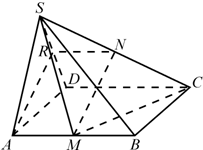
所以MN∥AR,由于AR平面SAD,MN在平面SAD外,
所以MN∥平面SAD.(4分)
(Ⅱ)解法1:取AD的中点O,连结OS,过O作AD的垂线交BC于G,分别以OA,OG,OS为x,y,z轴,建立坐标系,
则C(-1,2,0),M(1,1,0),S(0,0,
),
=(2,-1,0),
=(1,1,-
),
设面SCM的法向量为
=(x,y,z),(6分)
则
,
令x=1,得
=(1,2,
),由已知得面ABCD的法向量
=(0,0,1),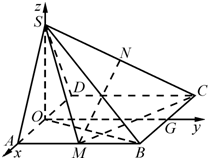 (8分)
(8分)
则cos<
,
>=
=
=
,
所以二面角S-CM-D的余弦值为
.(12分)
解法2:如图,取AD的中点O,连结OS、OB,OB∩CM=H,连结SH,由SO⊥AD,且面SAD⊥面ABCD,
所以SO⊥平面ABCD,SO⊥CM,
由已知得△ABO≌△BCM,所以∠ABO=∠BCM,
则∠BMH+∠ABO=∠BMH+∠BCM=90°,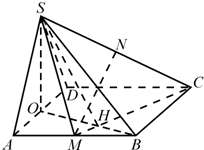
所以OB⊥CM,则有SH⊥CM,
所以∠SHO是二面角S-CM-D的平面角,
设AB=2,则OB=
,BH=
,OH=
,
OS=
,SH=
=
,
则cos∠SHO=
=
,
所以二面角S-CM-D的余弦值为
.(12分)
解:(Ⅰ)如图,取SD的中点R,连结AR、RN,
则RN∥CD,且RN=
| 1 |
| 2 |
所以RN∥AM,且RN=AM,
所以四边形AMNR是平行四边形,

所以MN∥AR,由于AR平面SAD,MN在平面SAD外,
所以MN∥平面SAD.(4分)
(Ⅱ)解法1:取AD的中点O,连结OS,过O作AD的垂线交BC于G,分别以OA,OG,OS为x,y,z轴,建立坐标系,
则C(-1,2,0),M(1,1,0),S(0,0,
| 3 |
| CM |
| SM |
| 3 |
设面SCM的法向量为
| n1 |
则
|
令x=1,得
| n1 |
| 3 |
| n2 |
 (8分)
(8分)则cos<
| n1 |
| n2 |
| ||||
|
|
| ||
|
| ||
| 4 |
所以二面角S-CM-D的余弦值为
| ||
| 4 |
解法2:如图,取AD的中点O,连结OS、OB,OB∩CM=H,连结SH,由SO⊥AD,且面SAD⊥面ABCD,
所以SO⊥平面ABCD,SO⊥CM,
由已知得△ABO≌△BCM,所以∠ABO=∠BCM,
则∠BMH+∠ABO=∠BMH+∠BCM=90°,

所以OB⊥CM,则有SH⊥CM,
所以∠SHO是二面角S-CM-D的平面角,
设AB=2,则OB=
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
OS=
| 3 |
(
|
2
| ||
| 5 |
则cos∠SHO=
| OH |
| SH |
| ||
| 4 |
所以二面角S-CM-D的余弦值为
| ||
| 4 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
若α的终边与单位圆交于点(
,-
),则cosα=( )
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|