题目内容
当a为何值时,方程x3-3x2-a=0恰有一个实根、两个不等实根、三个不等实根或者有没有可能无实根?
考点:函数的零点与方程根的关系
专题:计算题,数形结合,分类讨论,导数的综合应用
分析:令函数f(x)=x3-3x2,求出函数的导数,令导数大于0,得增区间,令导数小于0,得减区间,进而得到极值,再作出直线y=a和y=x3-3x2,通过观察直线和曲线分别有0个交点、1个交点、2个交点和3个交点的情况即可.
解答:
 解:令函数f(x)=x3-3x2,则导数为
解:令函数f(x)=x3-3x2,则导数为
f′(x)=3x2-6x,
由f′(x)>0,解得,x>2或x<0,f(x)递增;
由f′(x)<0,解得,0<x<2,f(x)递减.
则有f(x)在x=0处取得极大值,且为0,
f(x)在x=2处取得极小值,且为-4.
方程x3-3x2-a=0,即有a=x3-3x2,
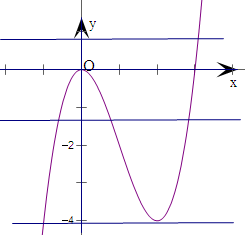
作出直线y=a和y=x3-3x2,
由于y=x3-3x2在(2,+∞),(-∞,0)内递增,
在(0,2)内递减,
则y=x3-3x2在x=0处取得极大值,且为0,
在x=2处取得极小值,且为-4.
通过图象观察,可得,当a>0或a<-4时,有1个交点,即f(x)有1个零点;
当a=0或-4,有2个交点,即f(x)有2个零点;
当-4<a<0,有3个交点,即f(x)有3个零点,
则不可能没有零点.
综上可得,当a>0或a<-4时,方程恰有一个实根;
当a=0或-4时,方程有两个不相等的实根;
当-4<a<0时,方程有3个实根;
不管a为何值,方程均有实根,不可能没有实根.
 解:令函数f(x)=x3-3x2,则导数为
解:令函数f(x)=x3-3x2,则导数为f′(x)=3x2-6x,
由f′(x)>0,解得,x>2或x<0,f(x)递增;
由f′(x)<0,解得,0<x<2,f(x)递减.
则有f(x)在x=0处取得极大值,且为0,
f(x)在x=2处取得极小值,且为-4.
方程x3-3x2-a=0,即有a=x3-3x2,
作出直线y=a和y=x3-3x2,
由于y=x3-3x2在(2,+∞),(-∞,0)内递增,
在(0,2)内递减,
则y=x3-3x2在x=0处取得极大值,且为0,
在x=2处取得极小值,且为-4.
通过图象观察,可得,当a>0或a<-4时,有1个交点,即f(x)有1个零点;
当a=0或-4,有2个交点,即f(x)有2个零点;
当-4<a<0,有3个交点,即f(x)有3个零点,
则不可能没有零点.
综上可得,当a>0或a<-4时,方程恰有一个实根;
当a=0或-4时,方程有两个不相等的实根;
当-4<a<0时,方程有3个实根;
不管a为何值,方程均有实根,不可能没有实根.
点评:本题考查函数的导数的运用:求单调区间和极值,考查函数的零点的求法,注意运用数形结合的思想方法,考查运算能力,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
下列函数中,是奇函数且在定义域内单调递增的函数是( )
A、y=-
| ||
| B、y=ex | ||
| C、y=x3-x | ||
D、y=-ln(
|
如图所示,全集U,集合A与集合B的关系,则集合B中阴影部分为( )


| A、∁U(A∩B) |
| B、(∁UA)∪B |
| C、(∁UA)∪(UB) |
| D、(∁UA)∩B |
已知实数1,m,9成等比数列,则圆锥曲线
+y2=1的离心率为( )
| x2 |
| m |
A、
| ||||||
| B、2 | ||||||
C、
| ||||||
D、
|
四棱锥P-ABCD的底面与侧面的形状和大小如图所示.
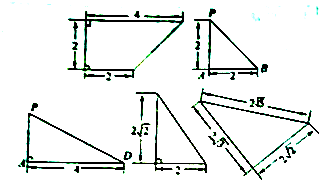
(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?

(1)画出该四棱锥的直观图,并证明:当E为PA的中点时,BE∥平面PCD;
(2)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?
设f(x)=
,则
f(x)dx等于( )
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |