题目内容
下列函数中,定义域是R且为增函数的是( )
| A、y=e-x |
| B、y=x |
| C、y=lnx |
| D、y=|x| |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据函数单调性的性质和函数成立的条件,即可得到结论.
解答:
解:A.函数的定义域为R,但函数为减函数,不满足条件.
B.函数的定义域为R,函数增函数,满足条件.
C.函数的定义域为(0,+∞),函数为增函数,不满足条件.
D.函数的定义域为R,在(0,+∞)上函数是增函数,在(-∞,0)上是减函数,不满足条件.
故选:B.
B.函数的定义域为R,函数增函数,满足条件.
C.函数的定义域为(0,+∞),函数为增函数,不满足条件.
D.函数的定义域为R,在(0,+∞)上函数是增函数,在(-∞,0)上是减函数,不满足条件.
故选:B.
点评:本题主要考查函数定义域和单调性的判断,比较基础.

练习册系列答案
相关题目
命题“?x∈[0,+∞),x3+x≥0”的否定是( )
| A、?x∈(-∞,0),x3+x<0 |
| B、?x∈(-∞,0),x3+x≥0 |
| C、?x0∈[0,+∞),x03+x0<0 |
| D、?x0∈[0,+∞),x03+x0≥0 |
定积分
(2x+ex)dx的值为( )
| ∫ | 1 0 |
| A、e+2 | B、e+1 |
| C、e | D、e-1 |
设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知角α的终边经过点(-4,3),则cosα=( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交于C于A,B两点,则|AB|=( )
A、
| ||||
| B、6 | ||||
| C、12 | ||||
D、7
|
 如图,在边长为1的正方形中随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为
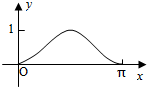
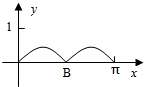
如图,在边长为1的正方形中随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为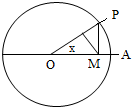 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P做直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P做直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为( )