题目内容
11. 如图直三棱柱中,△ABC是等腰直角三角形,AC⊥AB,AA′=AC=AB,A′C与B′C′所成的角是60度.
如图直三棱柱中,△ABC是等腰直角三角形,AC⊥AB,AA′=AC=AB,A′C与B′C′所成的角是60度.
分析 以A为原点,AB为x轴,AC为y轴,AA′为z轴,建立空间直角坐标系,利用向量法能求出A′C与B′C′所成的角.
解答  解:以A为原点,AB为x轴,AC为y轴,AA′为z轴,建立空间直角坐标系,
解:以A为原点,AB为x轴,AC为y轴,AA′为z轴,建立空间直角坐标系,
设AA′=AC=AB=1,
则A′(0,0,1),C(0,1,0),C′(0,1,1),B′(1,0,1),
$\overrightarrow{{A}^{'}C}=(0,1,-1)$,$\overrightarrow{{B}^{'}{C}^{'}}$=(-1,1,0),
设A′C与B′C′所成的角为θ,
则cosθ=$\frac{|\overrightarrow{{A}^{'}C}•\overrightarrow{{B}^{'}{C}^{'}}|}{|\overrightarrow{{A}^{'}C}|•|\overrightarrow{{B}^{'}{C}^{'}}|}$=$\frac{1}{2}$,
∴θ=60°.
故答案为:60.
点评 本题考查异面直线所成角的寺小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列命题中正确的是( )
| A. | 若一条直线垂直平面内的两条直线,则这条直线与这个平面垂直 | |
| B. | 若一条直线平行平面内的一条直线,则这条直线与这个平面平行 | |
| C. | 若一条直线垂直一个平面,则过这条直线的所有平面都与这个平面垂直 | |
| D. | 若一条直线与两条直线都垂直,则这两条直线互相平行 |
16.已知f(x)=sin(x+$\frac{π}{6}$),若sinα=$\frac{3}{5}$($\frac{π}{2}$<α<π),则f(α+$\frac{π}{12}$)=( )
| A. | $\frac{7\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{7\sqrt{2}}{10}$ |
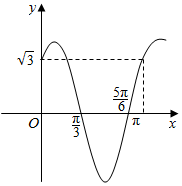 若函数y=Asin(ωx+φ)的图象如图所示,求它的解析式、频率和振幅.
若函数y=Asin(ωx+φ)的图象如图所示,求它的解析式、频率和振幅.