题目内容
6．
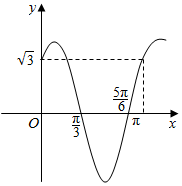若函数y=Asin（ωx+φ）的图象如图所示，求它的解析式、频率和振幅．
分析 根据三角函数的图象确定A，ω和φ的值即可得到结论．
解答 解：由图象可知函数的周期是π，即T=$\frac{2π}{ω}=π$，则ω=2，即函数的频率=$\frac{1}{T}$=$\frac{1}{π}$，
由五点对应法得2×$\frac{π}{3}$+φ=π，得φ=$\frac{π}{3}$，
即y=f（x）=Asin（2x+$\frac{π}{3}$），
∵f（0）=$\sqrt{3}$，
∴f（0）=Asin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$A=$\sqrt{3}$，得A=2，
即函数的解析式y=f（x）=2sin（2x+$\frac{π}{3}$），
故函数的振幅A=2，频率为$\frac{1}{π}$．
点评 本题主要考查三角函数解析式的求解，根据图象求出A，ω和φ的值是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
16．命题“?x∈R，都有log2x＞0成立”的否定为（ ）
| A． | ?x0∈R，使log2x0≤0成立 | B． | ?x0∈R，使log2x＞0成立 | ||
| C． | ?x∈R，都有log2x≥0成立 | D． | ?x∈R，都有log2x＞0成立 |
如图直三棱柱中，△ABC是等腰直角三角形，AC⊥AB，AA′=AC=AB，A′C与B′C′所成的角是60度．