题目内容
16.已知抛物线C1:y2=2x与椭圆C2:$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1在第一象限交于点A,直线y=$\sqrt{2}$x+m与椭圆C2交于B、D两点,且A,B,D三点两两互不重合.(1)求m的取值范围;
(2)△ABD的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
分析 (1)联立方程中先求出A点坐标,联立方程组$\left\{\begin{array}{l}y=\sqrt{2}x+m\\ 2{x^2}+{y^2}=4\end{array}\right.,得4{x^2}+2\sqrt{2}mx+{m^2}-4=0$,由此利用根的判别式能求出m的取值范围.
(2)利用椭圆弦长公式和点到直线的距离公式能求出当m=±2时,△ABD的面积最大,最大值为$\sqrt{2}$.
解答 解:(1)∵抛物线C1:y2=2x与椭圆C2:$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1在第一象限交于点A,
∴由$\left\{\begin{array}{l}{{y}^{2}=2x}\\{\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得A点坐标为$(1,\sqrt{2})$,(1分)
联立方程组$\left\{\begin{array}{l}y=\sqrt{2}x+m\\ 2{x^2}+{y^2}=4\end{array}\right.,得4{x^2}+2\sqrt{2}mx+{m^2}-4=0$,(3分)
∵A、B、D三点两两互不重合,
∴△=-8m2+64>0,∴$-2\sqrt{2}<m<2\sqrt{2}$,且m≠0,
∴m的取值范围是$(-2\sqrt{2},0)∪(0,2\sqrt{2})$.(6分)
(2)设B(x1,y1),D(x2,y2),${x_1}+{x_2}=-\frac{{\sqrt{2}m}}{2},{x_1}{x_2}=\frac{{{m^2}-4}}{4}$ ①
∵|BD|=$\sqrt{1+(\sqrt{2})^{2}}$|x1-x2|=$\frac{\sqrt{6}}{2}$$\sqrt{8-{m}^{2}}$,(9分)
设d为点A到直线BD$y=\sqrt{2}x+m$的距离,则$d=\frac{\left|m\right|}{{\sqrt{3}}}$.(10分)
∴${S_{△ABD}}=\frac{1}{2}•\left|{BD}\right|•d=\frac{{\sqrt{2}}}{4}\sqrt{(8-m{\;}^2){m^2}}≤\sqrt{2}$,当且仅当m=±2时取等号.
∵±2∈(-2$\sqrt{2}$,0)∪(0,2$\sqrt{2}$),
∴当m=±2时,△ABD的面积最大,最大值为$\sqrt{2}$.(12分)
点评 本题考查实数的取值范围的求法,考查三角形的最大值是否存在的判断与求法,是中档题,解题时要认真审题,注意根的判别式、椭圆弦长公式和点到直线的距离公式的合理运用.

 如图,空间四边形OABC中,点M在OA上,且OM=2MA,点N为BC中点,$\overrightarrow{MN}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x,y,z的值分别是( )
如图,空间四边形OABC中,点M在OA上,且OM=2MA,点N为BC中点,$\overrightarrow{MN}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x,y,z的值分别是( )| A. | $-\frac{2}{3},\frac{1}{2},\frac{1}{2}$ | B. | $\frac{1}{2},-\frac{2}{3},\frac{1}{2}$ | C. | $\frac{1}{2},\frac{1}{2},-\frac{1}{2}$ | D. | $\frac{2}{3},\frac{2}{3},-\frac{1}{2}$ |
| A. | Q<P<R | B. | P<Q<R | C. | Q<R<P | D. | P<R<Q |
| A. | $\frac{{\sqrt{14}}}{2}-1$ | B. | $\frac{{\sqrt{15}}}{2}-1$ | C. | 2 | D. | $\sqrt{5}-1$ |
 如图直三棱柱中,△ABC是等腰直角三角形,AC⊥AB,AA′=AC=AB,A′C与B′C′所成的角是60度.
如图直三棱柱中,△ABC是等腰直角三角形,AC⊥AB,AA′=AC=AB,A′C与B′C′所成的角是60度.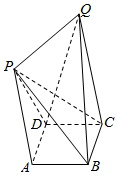 如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.
如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.