题目内容
19.化简求值:(1)sin14°cos16°+sin76°•cos74°;
(2)sin(54°-x)cos(36°+x)+cos(54°-x)sin(36°+x);
(3)sin$\frac{π}{12}$-$\sqrt{3}$cos$\frac{π}{12}$.
分析 分别根据两角和与差的正弦公式,以及诱导公式,化简计算即可.
解答 解:(1)sin14°cos16°+sin76°•cos74°=sin14°cos16°+cos14°•sin16°=sin30°=$\frac{1}{2}$,
(2)sin(54°-x)cos(36°+x)+cos(54°-x)sin(36°+x)=sin(54°-x+36°+x)=sin90°=1,
(3)sin$\frac{π}{12}$-$\sqrt{3}$cos$\frac{π}{12}$=2($\frac{1}{2}$sin$\frac{π}{12}$-$\frac{\sqrt{3}}{2}$cos$\frac{π}{12}$)=2(cos$\frac{π}{3}$sin$\frac{π}{12}$-sin$\frac{π}{3}$cos$\frac{π}{12}$)=2sin($\frac{π}{12}$-$\frac{π}{3}$)=-2sin$\frac{π}{4}$=-$\sqrt{2}$.
点评 本题考查了两角和与差的正弦公式,以及诱导公式,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图直三棱柱中,△ABC是等腰直角三角形,AC⊥AB,AA′=AC=AB,A′C与B′C′所成的角是60度.
如图直三棱柱中,△ABC是等腰直角三角形,AC⊥AB,AA′=AC=AB,A′C与B′C′所成的角是60度.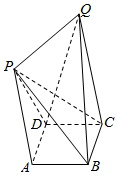 如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.
如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.