题目内容
已知x2+y2=4的圆内有P与A(-2,0),B(2,0),连接PA、PB,|
|•|
|=|
|2.求
•
范围.(运用
•
=|
|•|
|•cosθ求解)
| PA |
| PB |
| PO |
| PA |
| PB |
| PA |
| PB |
| PA |
| PB |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用,直线与圆
分析:由|
|•|
|=|
|2,设点P(x,y),代入化简可得x2=y2+2.由点P在圆内可得 x2+y2<4,可得0≤y2<1.化简
•
=2(y2-1),从而求得
•
的取值范围.
| PA |
| PB |
| PO |
| PA |
| PB |
| PA |
| PB |
解答:
解:圆O与x轴相交于A(-2,0)、B(2,0)两点,
圆内的动点P满足|
|•|
|=|
|2,
设点P(x,y),
则有
•
=x2+y2,
即
=x2+y2,
两边平方,化简可得 x2=y2+2.
由点P在圆内可得 x2+y2<4,故有 0≤y2<1.
∵
•
=(-2-x,-y)•(2-x,-y)=x2+y2-4=2(y2-1)∈[-2,0).
即
•
的取值范围是[-2,0).
圆内的动点P满足|
| PA |
| PB |
| PO |
设点P(x,y),
则有
| (x+2)2+y2 |
| (x-2)2+y2 |
即
| (x2+y2+4)2-(4x)2 |
两边平方,化简可得 x2=y2+2.
由点P在圆内可得 x2+y2<4,故有 0≤y2<1.
∵
| PA |
| PB |
即
| PA |
| PB |
点评:本题主要考查直线和圆的位置关系,两个向量的数量积的定义和坐标表示,属于中档题.

练习册系列答案
相关题目
如图是y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象的一段,则其解析式为( )


A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
已知底面边长为2,侧棱长为2
,则正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、2π | ||
D、
|
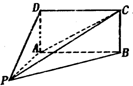 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.