题目内容
若a,b,c满足P=a+b-c,Q=b+c-a,R=c+a-b,则“P•Q•R>0”是“P、Q、R同时大于零”的 条件.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:P•Q•R>0,可以有两项都小于0,而另一项大于0,可以举一个这样的例子:取a=-1,b=-2,c=-4,用这个例子即可说明由P•Q•R>0得不到P,Q,R同时大于零;而P,Q,R同时大于零时,显然可得到P•Q•R>0,所以得到“P•Q•R>0”是“P、Q、R同时大于零”的必要不充分条件.
解答:
解:(1)由P•Q•R>0得不到P、Q、R同时大于零,比如a=-1,b=-2,c=-4,则有:
a+b-c=1,b+c-b=-5,c+a-b=-3,∴满足P•Q•R>0,而P,Q,R不全大于0;
∴“P•Q•R>0”不是“P,Q,R同时大于0”的充分条件;
(2)P,Q,R同时大于0时,显然能得到P•Q•R>0;
∴“P•Q•R>0”是“P、Q、R同时大于”0的必要条件;
总上得“P•Q•R>0”是“P、Q、R同时大于零”的必要不充分条件.
故答案为:必要不充分.
a+b-c=1,b+c-b=-5,c+a-b=-3,∴满足P•Q•R>0,而P,Q,R不全大于0;
∴“P•Q•R>0”不是“P,Q,R同时大于0”的充分条件;
(2)P,Q,R同时大于0时,显然能得到P•Q•R>0;
∴“P•Q•R>0”是“P、Q、R同时大于”0的必要条件;
总上得“P•Q•R>0”是“P、Q、R同时大于零”的必要不充分条件.
故答案为:必要不充分.
点评:考查举反例的方法说明由一个条件得不到另一个条件,以及充分条件、必要条件、必要不充分条件的概念.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
若关于x的方程mx2+(2m+1)x+m=0有两个不相等的实数根,则m的取值范围是( )
A、m<-
| ||
B、m>-
| ||
C、m<-
| ||
D、m>-
|
若不等式x2-
x≥0对任意实数x都成立,则实数a的取值是( )
| a |
| A、{0} | B、{0,1} |
| C、(0,1) | D、[0,+∞) |
已知在某班有
的学生数学成绩优秀,如果从班中随机地找出5名学生,那么其中数学成绩优秀的学生X~B(5,
),则E(-X)的值为( )
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知
、
是两个不平行的非零向量,并且
∥
,
∥
,则向量
等于( )
| a |
| b |
| a |
| c |
| b |
| c |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|

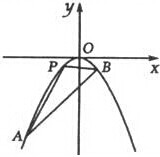 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,