题目内容
19．在等差数列{an}中，若a2=3，a5=9，则其前6项和S6=（ ）| A． | 12 | B． | 24 | C． | 36 | D． | 48 |
分析 利用等差数列的通项公式及其前n项和公式即可得出．
解答 解：设等差数列{an}的公差为d，
∵a2=3，a5=9，
∴$\left\{\begin{array}{l}{{a}_{1}+d=3}\\{{a}_{1}+4d=9}\end{array}\right.$，
解得d=2，a1=1．
则其前6项和S6=6+$\frac{6×5}{2}$×2=36．
故选：C．
点评 本题考查了等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．在等差数列{an}中，若a4+a6+a8+a10+a12=120，则2a10-a12的值为（ ）
| A． | 6 | B． | 12 | C． | 24 | D． | 60 |
7．执行如图所示的程序框图，输出的x值为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
4．i是虚数单位，复数$\frac{2}{1+i}$的共轭复数是（ ）
| A． | 1+i | B． | 1-i | C． | 2+2i | D． | 2-2i |
11．
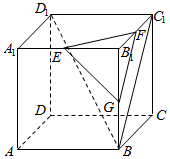在正方体ABCD-A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，给出下列四个推断：
①FG∥平面AA1D1D； ②EF∥平面BC1D1；
③FG∥平面BC1D1； ④平面EFG∥平面BC1D1
其中推断正确的序号是（ ）
在正方体ABCD-A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，给出下列四个推断：①FG∥平面AA1D1D； ②EF∥平面BC1D1；
③FG∥平面BC1D1； ④平面EFG∥平面BC1D1
其中推断正确的序号是（ ）
| A． | ①③ | B． | ①④ | C． | ②③ | D． | ②④ |
8．设$f（x）={e^{\frac{1}{2}x}}$（x-1）-ax+2a恰有小于1两个零点，则a的取值范围是（ ）
| A． | $（0，\frac{1}{2}）$ | B． | $（0，\frac{2}{{3\sqrt{e}}}）$ | C． | $（-∞，\frac{1}{2}]$ | D． | $（-∞，\frac{2}{{3\sqrt{e}}}]$ |