题目内容
8.设$f(x)={e^{\frac{1}{2}x}}$(x-1)-ax+2a恰有小于1两个零点,则a的取值范围是( )| A. | $(0,\frac{1}{2})$ | B. | $(0,\frac{2}{{3\sqrt{e}}})$ | C. | $(-∞,\frac{1}{2}]$ | D. | $(-∞,\frac{2}{{3\sqrt{e}}}]$ |
分析 令f(x)=0,使用分离参数法得a=$\frac{{e}^{\frac{1}{2}x}(x-1)}{x-2}$,则令g(x)=$\frac{{e}^{\frac{1}{2}x}(x-1)}{x-2}$,求出g(x)在(-∞,1)上的值域.则根据a=g(x)有两解得出a的范围.
解答 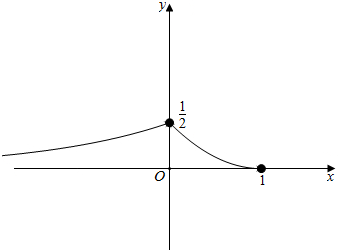 解:令f(x)=0得e${\;}^{\frac{1}{2}x}$(x-1)=ax-2a,∴a=$\frac{{e}^{\frac{1}{2}x}(x-1)}{x-2}$.令g(x)=$\frac{{e}^{\frac{1}{2}x}(x-1)}{x-2}$.则g′(x)=$\frac{(\frac{1}{2}{e}^{\frac{1}{2}x}(x-1)+{e}^{\frac{1}{2}x})(x-2)-{e}^{\frac{1}{2}x}(x-1)}{(x-2)^{2}}$=e${\;}^{\frac{1}{2}x}$$•\frac{x}{2(x-2)^{2}}$•(x-3).
解:令f(x)=0得e${\;}^{\frac{1}{2}x}$(x-1)=ax-2a,∴a=$\frac{{e}^{\frac{1}{2}x}(x-1)}{x-2}$.令g(x)=$\frac{{e}^{\frac{1}{2}x}(x-1)}{x-2}$.则g′(x)=$\frac{(\frac{1}{2}{e}^{\frac{1}{2}x}(x-1)+{e}^{\frac{1}{2}x})(x-2)-{e}^{\frac{1}{2}x}(x-1)}{(x-2)^{2}}$=e${\;}^{\frac{1}{2}x}$$•\frac{x}{2(x-2)^{2}}$•(x-3).
令g′(x)=0,得x=0或x=3.
当x<0时,g′(x)>0,当0<x≤1时,g′(x)<0,∴g(x)在(-∞,0)上是增函数,在(0,1]上是减函数,
∵$\underset{lim}{n→-∞}g(x)=0$,g(0)=$\frac{1}{2}$,g(1)=0,∴g(x)在(-∞,1)上的值域为(0,$\frac{1}{2}$].
作出g(x)在(-∞,1)上函数的大致图象如图:
∵$f(x)={e^{\frac{1}{2}x}}$(x-1)-ax+2a恰有小于1两个零点,∴a=g(x)在(-∞,1)上有两解.
∴0<a$<\frac{1}{2}$.
故选A.
点评 本题考查了函数的单调性,函数的值域,零点的个数判断,借助函数图象可比较方便的得出结论.

| A. | 12 | B. | 24 | C. | 36 | D. | 48 |