题目内容
已知参数方程
(1)若t为常数θ为参数,判断方程表示什么曲线
(2)若θ为常数t为参数,方程表示什么曲线.
|
(1)若t为常数θ为参数,判断方程表示什么曲线
(2)若θ为常数t为参数,方程表示什么曲线.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)首先,把sinθ和cosθ表示出来,然后,平方相加,消去θ,从而得到普通方程,再根据普通方程确定其曲线形状;
(2)首先,求解得到
,然后,平方相减,代人消去t,即得普通方程,然后,确定曲线形状.
(2)首先,求解得到
|
解答:
解:(1)根据参数方程
,消去θ,即
①2+②2,得
(
)2+(
)2=1,
它表示一个椭圆.
(2)由θ为常数t为参数,消去t,得
,两式平方相减,得
-
=4,
它表示一个焦点在x轴上的双曲线.
|
①2+②2,得
(
| x | ||
t+
|
| y | ||
t-
|
它表示一个椭圆.
(2)由θ为常数t为参数,消去t,得
|
| x2 |
| sin2θ |
| y2 |
| cos2θ |
它表示一个焦点在x轴上的双曲线.
点评:本题重点考查了参数方程和普通方程的互化,及互化原则,常见曲线的特征等知识,属于中档题.

练习册系列答案
相关题目
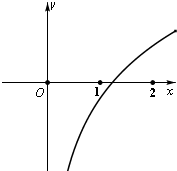
如图为函数f(x)=t+logax的图象(a,t均为实常数),则下列结论正确的是 ( )

| A、0<a<1,t<0 |
| B、0<a<1,t>0 |
| C、a>1,t<0 |
| D、a>1,t>0 |
已知|
|=
,
=(1-λ)
+λ
,若
•
=0,
•
=1,则λ=( )
| a |
| 2 |
| c |
| a |
| b |
| a |
| b |
| a |
| c |
| A、1 | ||
B、-
| ||
C、
| ||
| D、-1 |
如图所示,程序执行后的输出结果为( )


| A、-1 | B、0 | C、1 | D、2 |
已知条件p:x>0,条件q:x≥1,则p是q成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
 已知f(x)=|x+a|(a>-2)的图象过点(2,1).
已知f(x)=|x+a|(a>-2)的图象过点(2,1).