题目内容
已知函数 ,正实数
,正实数 满足
满足 ,且
,且 ,若
,若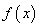 在区间
在区间
 上的最大值为2,则
上的最大值为2,则
2

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
题目内容
已知函数 ,正实数
,正实数 满足
满足 ,且
,且 ,若
,若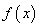 在区间
在区间
 上的最大值为2,则
上的最大值为2,则
2

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案